Dynamical systems

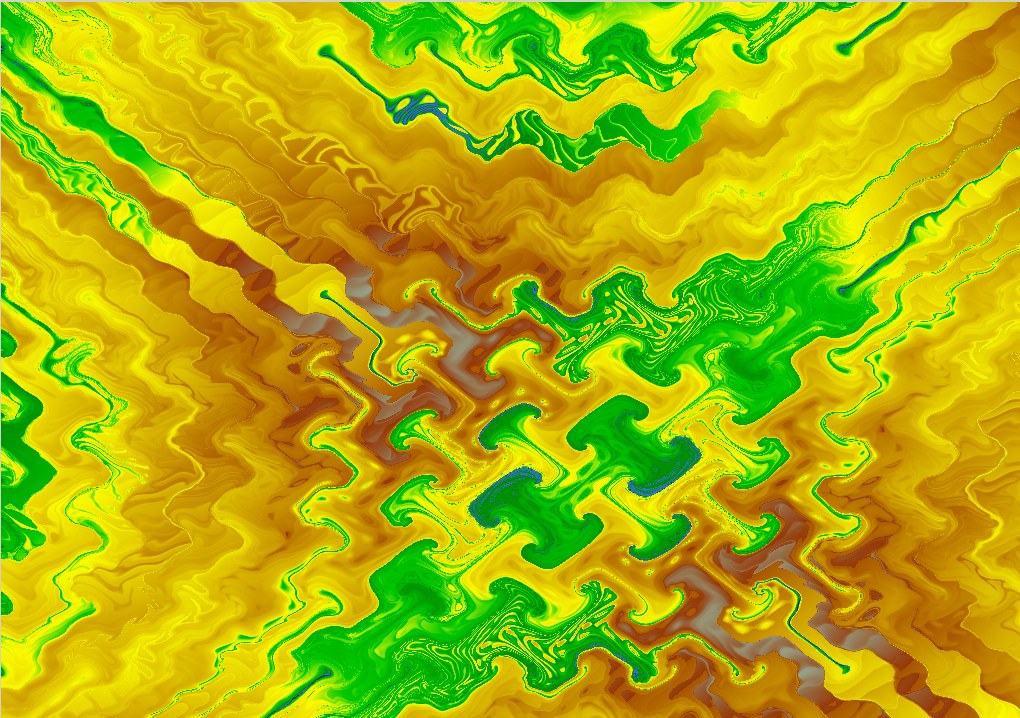
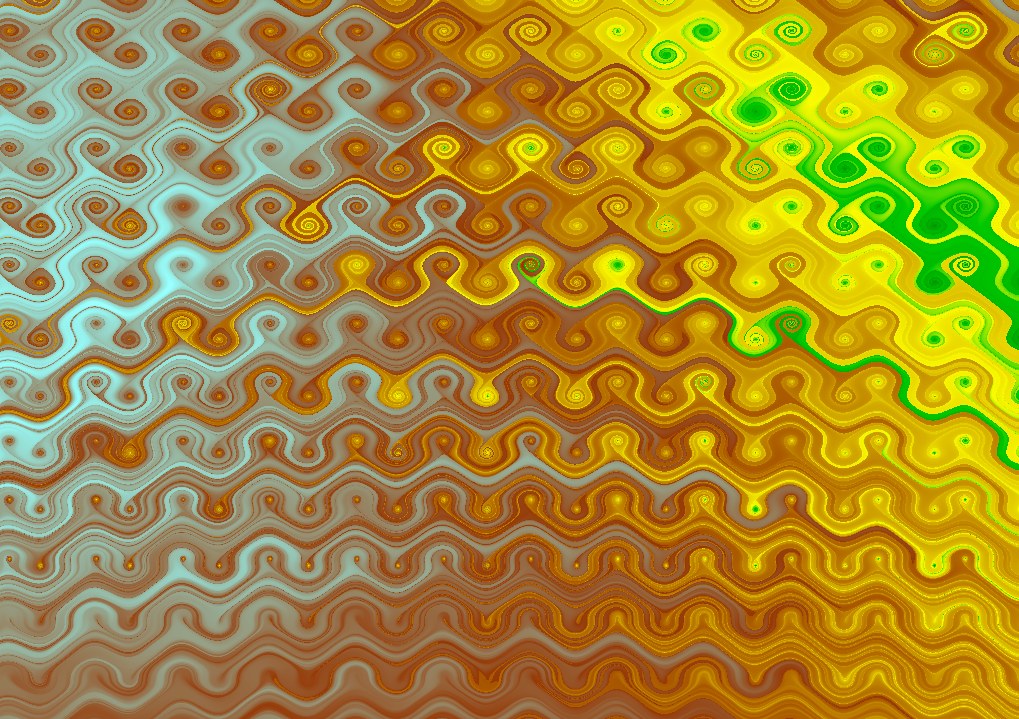
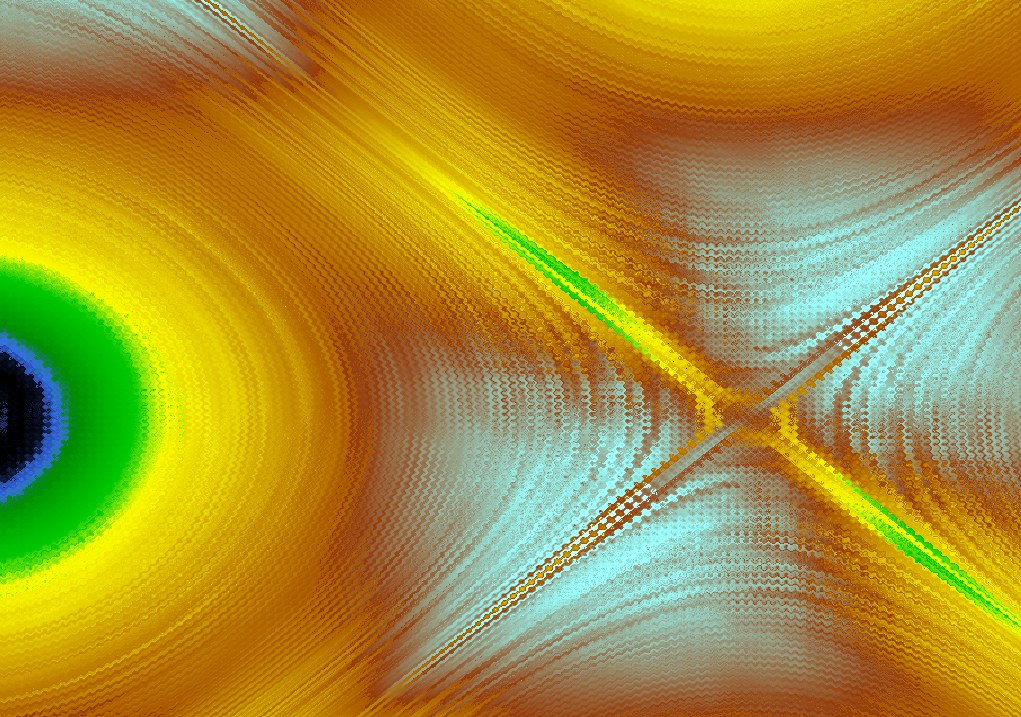
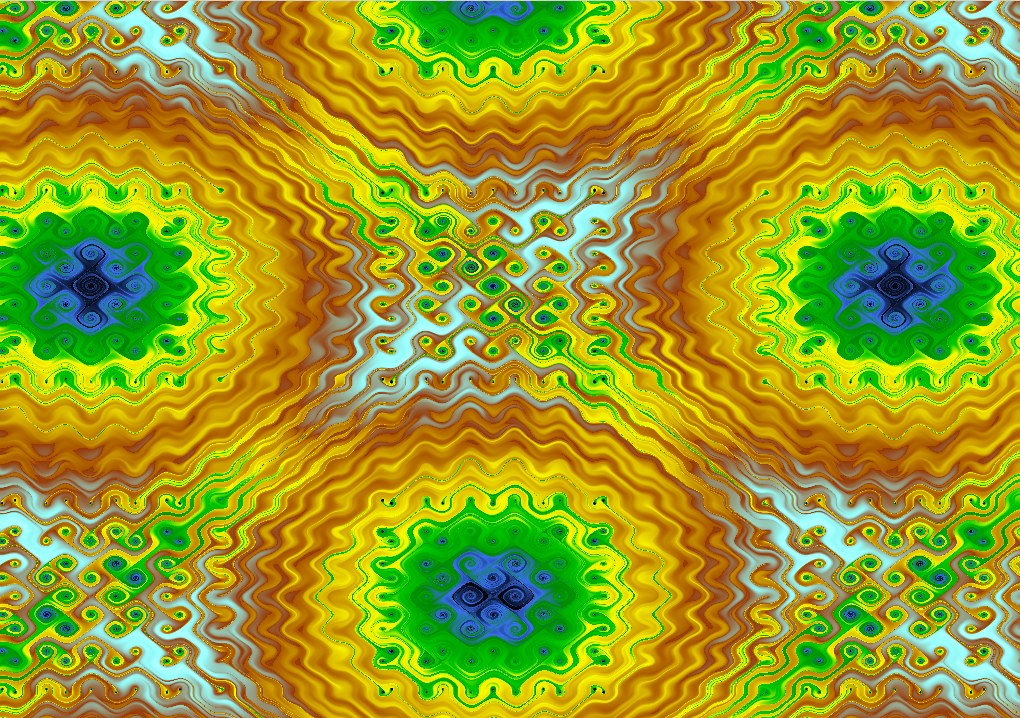
These images were made by mucking around with equations producing (to quote from the Pickover chapter that inspired them) “time-discrete phase planes associated with the cyclic systems:

(1) $\begin{equation*} \left\{ \begin{array} {lr} \dot{x}(t)=-f(y(t))\qquad \longleftarrow\quad \dot{x}(t)\text{ means the rate of change of }x\text{ at time }t,\\ \dot{y}(t)=f(x(t))\qquad\qquad\qquad \text{like the speed of a car at a certain moment }t.\\ \end{array} \right. \end{equation*}$

In phase space each dimension can represent one of the variables in the differential equation. …Here, these functions are generally of the form often found in frequency modulation synthesis applications:

$f(x)=\sin[x+\sin(\rho x)]$

By modulating a sine wave (often called the “carrier”) by another with a different frequency (controlled by $\rho$ ), a large variety of complex waveforms can be generated … Using this technique, a graphically “rich” function can be produced with only a small number of input parameters.
The discretization of Equation $(1)$ for implementation on a computer takes the following simple form (known as the forward Euler approximation):

$\left\{ \begin{array}{lr} x_{t+1}-x_t=-hf(y_t)\\ y_{t+1}-y_t=hf(x_t) \end{array} \right.$

where $h>0$ is a constant known as the step size of the numerical solution. In this section, $h$ is kept small ( $h\sim0.1$ ). … Despite the phase portraits’ complexity, they possess universal features shared by entire classes of nonlinear processes. For example, a range of real physical systems can be described by similar systems of differential equations.” ${}^1$
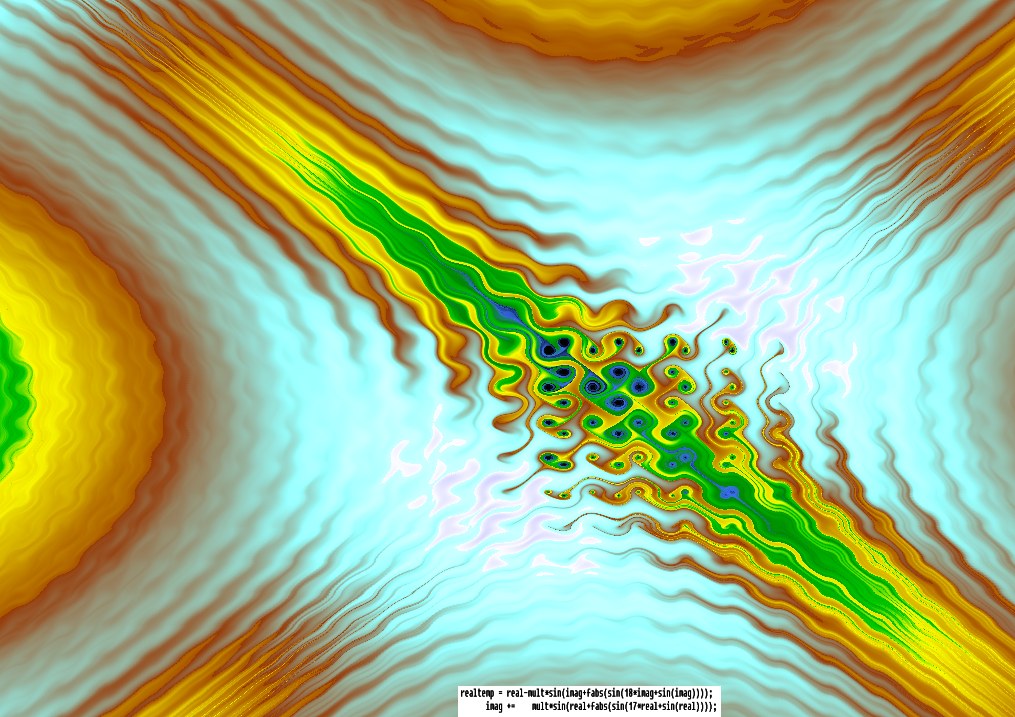
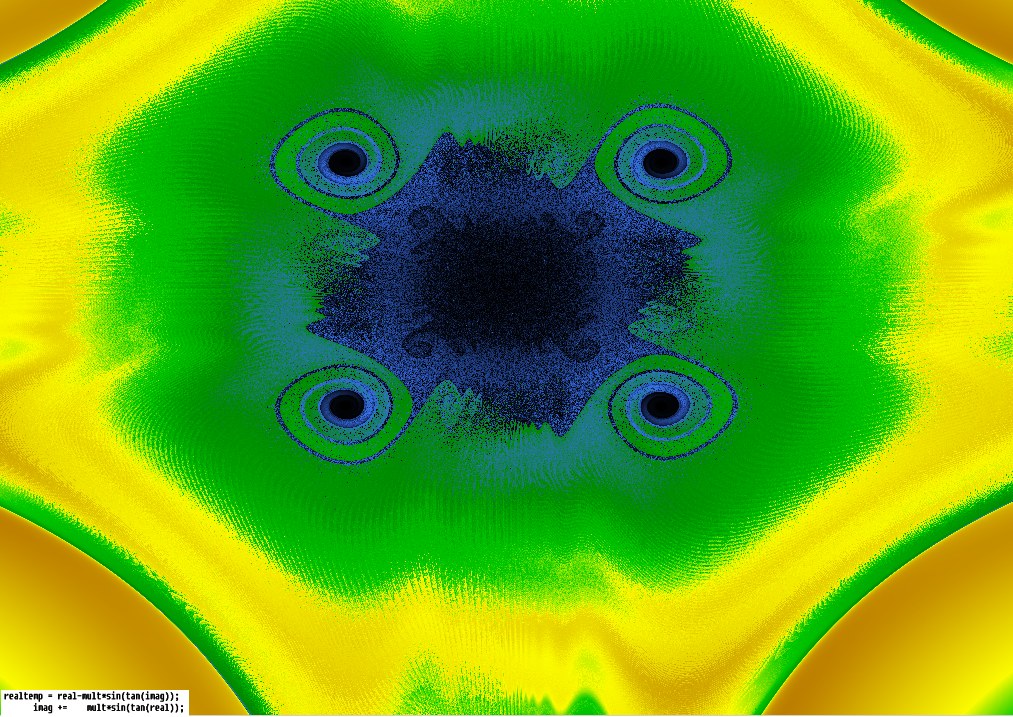
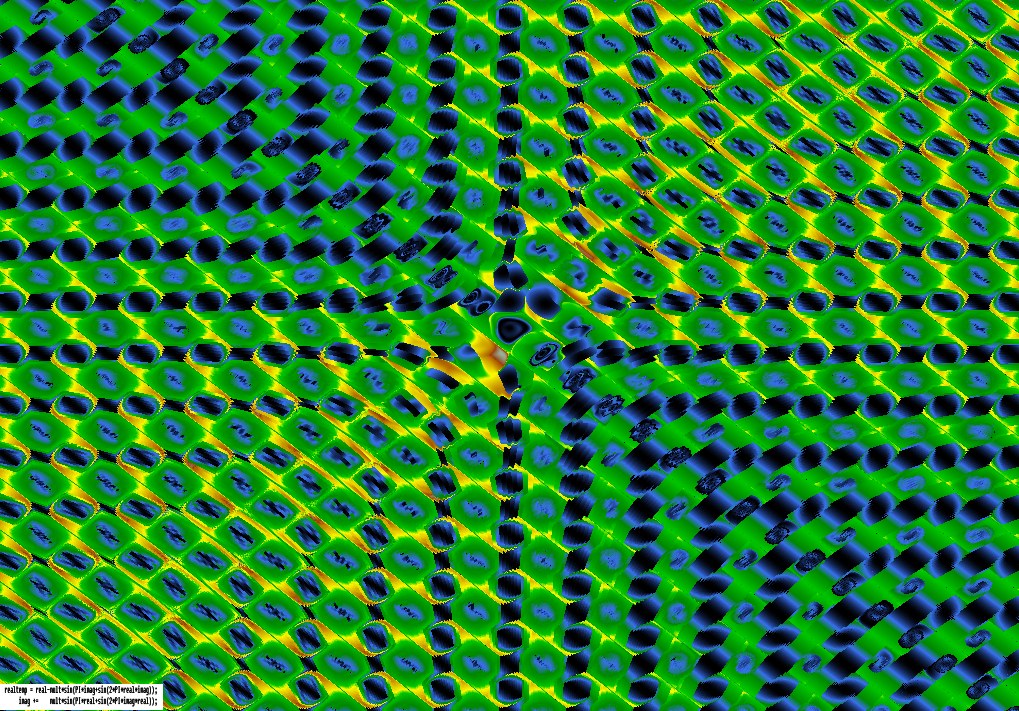
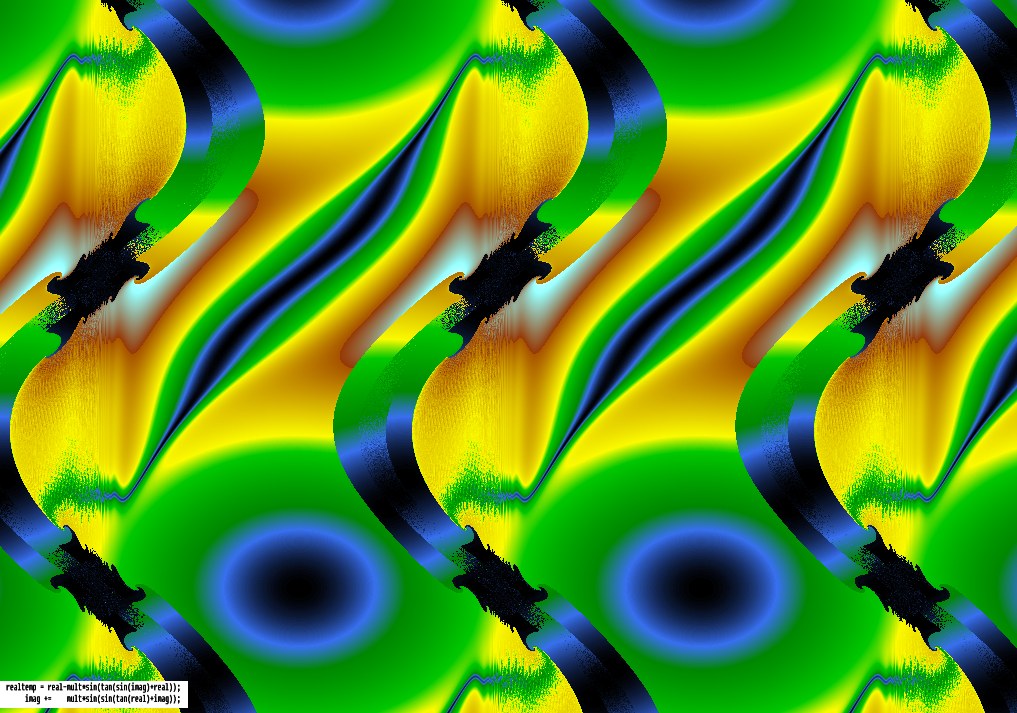
I’ve not used the trajectories of randomly-chosen points, as he does, but instead traced the trajectory of every point on the screen a certain small number of steps, and colouring them according to the distance travelled from the starting point, with colours similar to those used in coloured relief maps – blue(ocean) $\rightarrow$ dark green $\rightarrow$ light green $\rightarrow$ yellow $\rightarrow$ brown $\rightarrow$ white(snow).
Some of the images have the 2 main equation lines pasted on them, from the program that drew them – e.g. the 11th picture below, the first one with a formula on it, says in C++ :
realtemp = real-mult*sin(27*imag+sin(7*imag));
imag += mult*sin(30*real+sin(28*real));
I made those numbers up pretty much randomly, to see what would happen. This translates into the above style as: