more on CFs

warning: page of speculation and wondering

In “Euclidean” algorithm form:

    \begin{align*} \sqrt{3} &\approx 1.7 \\ \frac{1}{\sqrt{3}-1}&=\frac{\sqrt{3}+1}{(\sqrt{3}-1)(\sqrt{3}+1)}=\frac{\sqrt{3}+1}{2} \end{align*}

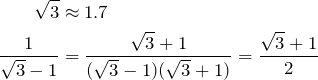
And now we put on top not the usual 1/ of a regular CF, but 2/, to cancel the denominator.

    \begin{align*} \frac{2(\sqrt{3}+1)}{2}&=\sqrt{3}+1 \approx 2.7 \\ \frac{1}{\sqrt{3}+1-2}&=\frac{1}{\sqrt{3}-1} \end{align*}

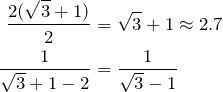
And here we have the same fraction as before, so the terms will repeat, i.e.

    \[\sqrt{3}=1+\cfrac{2}{2+\cfrac{2}{2+\cfrac{2}{2+\dots}}}\]

A formula for nonregular CFs of square roots

    \begin{align*} \text{If }\quad x&= 1+\cfrac{a}{2+\cfrac{a}{2+\cfrac{a}{2+\cfrac{a}{2+\dots}}}} \\ \text{then }\quad x+1&= 2+\cfrac{a}{2+\cfrac{a}{2+\cfrac{a}{2+\cfrac{a}{2+\dots}}}} \\ \text{So }\quad x &=1+\frac{a}{x+1} \\ \text{i.e. }\quad (x-1)(x+1)&=a \\ x^2-1&=a \\ x&=\sqrt{a+1} \\ \text{So }\quad \sqrt{a+1}&=1+\cfrac{a}{2+\cfrac{a}{2+\cfrac{a}{2+\dots}}} \end{align*}

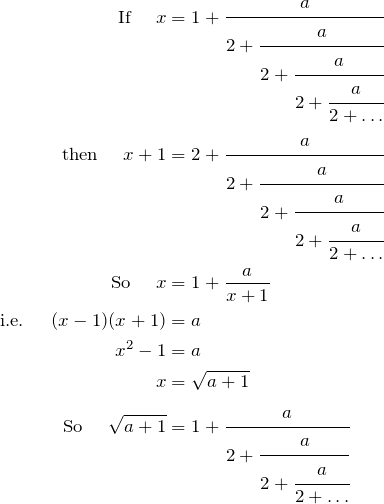
Using the formula, and the Euclidean method above:

    \[\sqrt{17}=1+\cfrac{16}{2+\cfrac{16}{2+\cfrac{16}{2+\dots}}}=4+\cfrac{1}{4+\cfrac{1}{4+\dots}}\]

references

CF links

wikipedia
contfrac CF computer
Gosper’s CF arithmetic
Gosper HAKMEM
mathworld
fractional iteration of 1/(1+x)

Leave a Reply

Your email address will not be published. Required fields are marked *