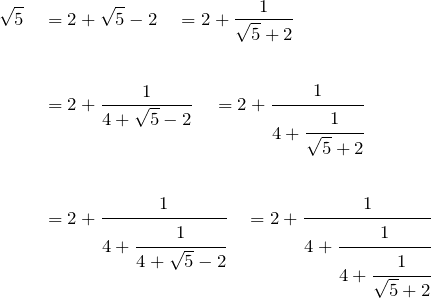Some easily constructed continued fractions

Continued fractions of square roots are infinite (they go on forever) but repeating. And so are all quadratic irrationals – numbers that arise as solutions of quadratic equations – i.e. of the form ax^2+bx+c=0

Some irrational continued fractions, of the form \sqrt{m^2+1}, can be built with almost no calculation whatsoever.
These are \sqrt{2}, \sqrt{5}, \sqrt{10}, \sqrt{17}, \sqrt{26}, \sqrt{37}, \sqrt{50}, \sqrt{65}\dots

The constructions rely totally on multiplication by conjugate surds. If that sounds unfamiliar, read the very short explanation of using conjugate surds.

The case of \sqrt{2} involves continually multiplying \sqrt{2}-1 by \displaystyle \frac{\sqrt{2}+1}{\sqrt{2}+1} to get \displaystyle \frac{1}{\sqrt{2}+1}.
(Usually conjugate surds are used to get the \sqrt to the top!)
Then 1s and 2s are shifted around to make another \sqrt{2}-1 to repeat the process:

    \begin{align*} \sqrt{2} \quad &= 1+\sqrt{2}-1 \quad = 1+\frac{1}{\sqrt{2}+1} \\ \\ &= 1+\frac{1}{2+\sqrt{2}-1} \quad = 1+\cfrac{1}{2+\cfrac{1}{\sqrt{2}+1}}\\ \\ &= 1+\cfrac{1}{2+\cfrac{1}{2+\sqrt{2}-1}} \quad = 1+\cfrac{1}{2+\cfrac{1}{2+\cfrac{1}{\sqrt{2}+1}}}\\ \\ &= 1+\cfrac{1}{2+\cfrac{1}{2+\cfrac{1}{2+\sqrt{2}-1}}} \quad = 1+\cfrac{1}{2+\cfrac{1}{2+\cfrac{1}{2+\cfrac{1}{\sqrt{2}+\dots}}}}\\ \end{align*}

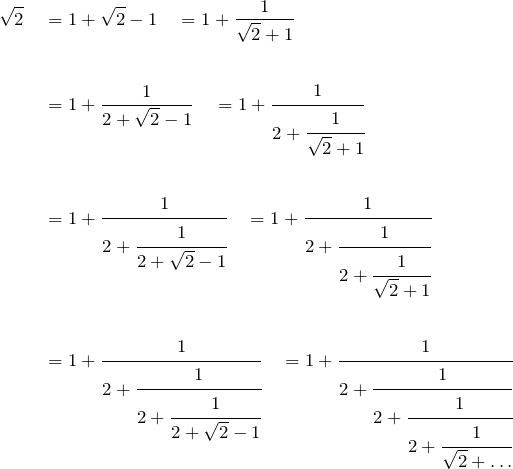
Obviously that may go on for some time.

The continued fraction for \sqrt{5} uses the fact that \displaystyle \sqrt{5}-2 = \frac{1}{\sqrt{5}+2}.

    \begin{align*} \sqrt{5} \quad &= 2+\sqrt{5}-2 \quad = 2+\frac{1}{\sqrt{5}+2} \\ \\ &= 2+\frac{1}{4+\sqrt{5}-2} \quad = 2+\cfrac{1}{4+\cfrac{1}{\sqrt{5}+2}}\\ \\ &= 2+\cfrac{1}{4+\cfrac{1}{4+\sqrt{5}-2}} \quad = 2+\cfrac{1}{4+\cfrac{1}{4+\cfrac{1}{\sqrt{5}+2}}}\\ \\\end{align*}

Leave a Reply

Your email address will not be published. Required fields are marked *