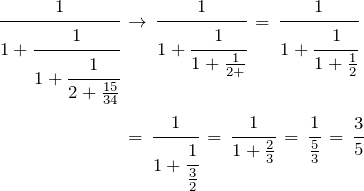(unfinished)
– why build scales from octaves and 5ths?
simple ratios of frequencies
– simple ratios, intervals, Pythagoras..
simplest ratios are x2 (octave) and x3 (oct + 5th)
*** why these sound good – the hear etc.. no beats.
*** ok, what is the sound of some other ratios that one might think may sound good?
pi, phi, root 2, e, 4/3 etc.
– simple ratios are primes, and so.. there’s always a pyth gap.
– going up in 5ths (3/2 times the freq)..
continued fractions
– have to approximate, adjust, fudge.. how best to do it? with continued fractions. This is a very useful technique, used, among other things, for finding best approximations of ratios with simple fractions, for example ![]() as an approximation for
as an approximation for ![]() – or
– or ![]() , known in ancient China, and accurate to within XXXXX – or finding good calendar systems, reconciling the incommensurable periods of the day, month and year.
, known in ancient China, and accurate to within XXXXX – or finding good calendar systems, reconciling the incommensurable periods of the day, month and year.
We have to find a particular number of octaves, call it ![]() , that’s very close to a particular number of 5ths, call it
, that’s very close to a particular number of 5ths, call it ![]() . i.e.
. i.e.
![]() number of octaves \approx
number of octaves \approx ![]() number of 5ths.
number of 5ths.
Since going up by octaves is the same as multiplying the frequency by 2 repeatedly, up 1 8ve is x2, up two is x2x2 or ![]() , up 3 octaves is x2x2x2 or
, up 3 octaves is x2x2x2 or ![]() , we can represent the frequency/pitch by
, we can represent the frequency/pitch by ![]() . Similarly the number of fifths we go up is
. Similarly the number of fifths we go up is ![]() lots of x3/2×3/2×3/2×3/2.. or
lots of x3/2×3/2×3/2×3/2.. or ![]()
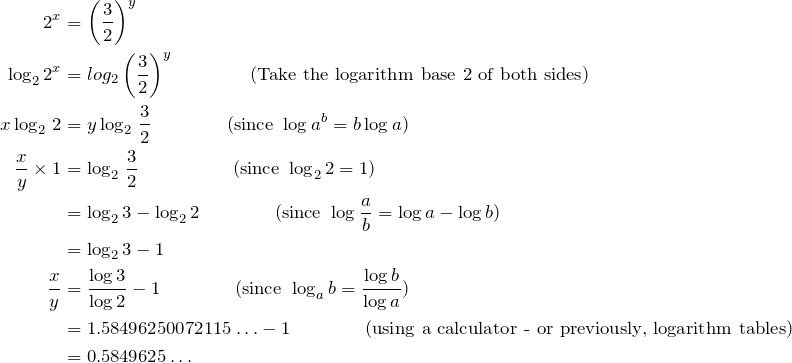
which is very close to ![]() – the difference is only
– the difference is only ![]() – less than 4 parts in 100,000.
– less than 4 parts in 100,000.
Which I believe is much more accuracy than is needed, and won’t make any difference to the result.
![]()
The next step is to turn ![]() into a continued fraction. It’s not so useful to know that 117 octaves is close to 200 fifths, unless you want an octave with 200 notes in it!
into a continued fraction. It’s not so useful to know that 117 octaves is close to 200 fifths, unless you want an octave with 200 notes in it!
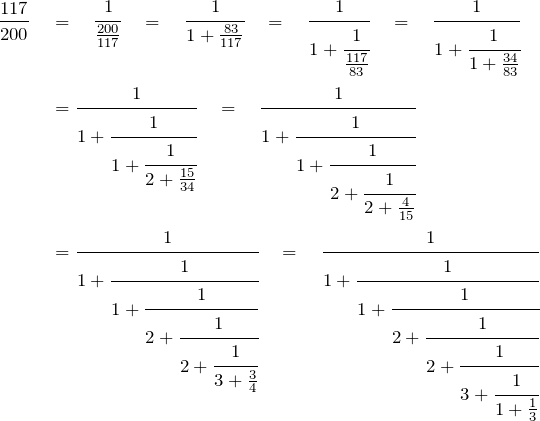
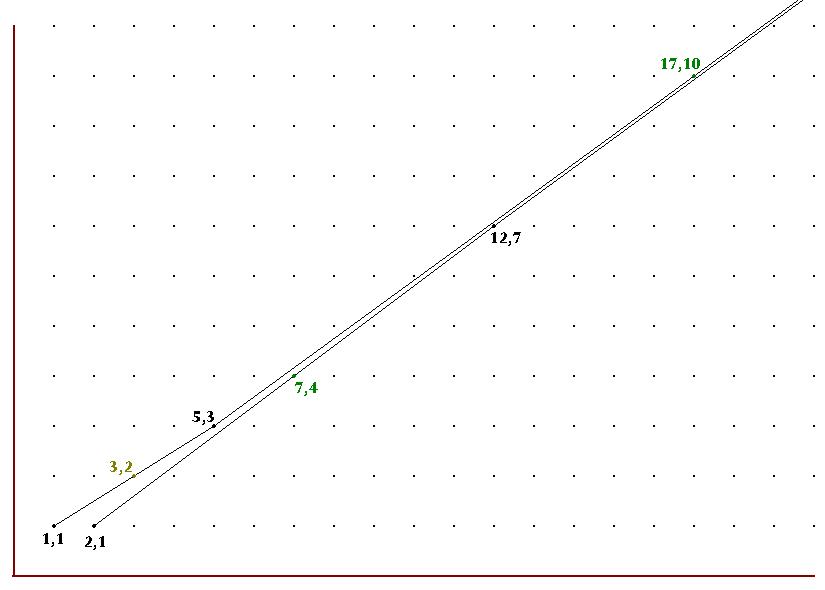
This is the same process as Euclid’s algorithm, and can be illustrated in a 200×117 rectangle:
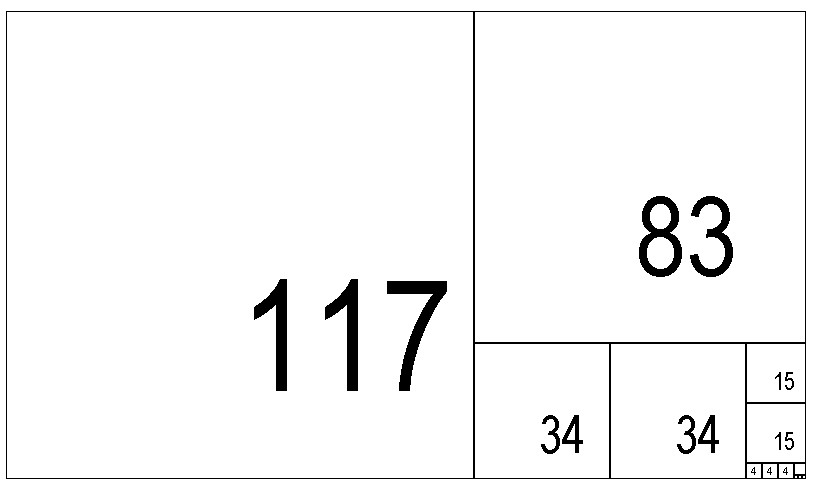
The successively closer approximations, convergents,are then gotten by using successively using more and of the continued fraction numbers.
The fractions that are produced, ![]() , will represent our sought-for quantities
, will represent our sought-for quantities ![]() and
and ![]() , of numbers of octaves, and numbers of fifths, that will be ‘assumed’ to be equal for our tuning.
, of numbers of octaves, and numbers of fifths, that will be ‘assumed’ to be equal for our tuning.
convergent 1 = 1.
convergent 2 = ![]()
So we start with the 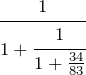 one, ignore the
one, ignore the ![]() part, and convert the rest back to a normal fraction:
part, and convert the rest back to a normal fraction: ![]()
So in this case, we have ![]() and
and ![]() – a scale with two ‘fifths’ in an octave (very flat ones!). Converting the other fractions we get:
– a scale with two ‘fifths’ in an octave (very flat ones!). Converting the other fractions we get: