Write a power series as:
![Rendered by QuickLaTeX.com \[f(x)=\sum^\infty_0\frac{a_n}{n!}x^n\]](https://www.adamponting.com/wp-content/ql-cache/quicklatex.com-86961e56ff6fb62872f94323016d3787_l3.png)
![]()
When ![]() , every term is
, every term is ![]() except the first, so
except the first, so ![]() .
.
Differentiate the series:
![]()
Now set ![]() and what remains is
and what remains is ![]() .
.
Differentiate again and get ![]() , and evidently
, and evidently ![]()
So the series can be written in the form:
![Rendered by QuickLaTeX.com \[\boxed{f(x)=\sum^\infty_0\frac{f^{(n)}(0)}{n!}x^n}\]](https://www.adamponting.com/wp-content/ql-cache/quicklatex.com-2294948a1bdcef45bec51ef74f0ebd44_l3.png)
This is the Maclaurin series.
If the derivatives are evaluated at ![]() instead, we get the Taylor series:
instead, we get the Taylor series:
![Rendered by QuickLaTeX.com \[\boxed{f(x)=\sum^\infty_0\frac{f^{(n)}(a)}{n!}(x-a)^n}\]](https://www.adamponting.com/wp-content/ql-cache/quicklatex.com-886676d67840769490788d3e6ba71f1d_l3.png)
series for ![]()
For the function ![]() etc.
etc.
At ![]() , since
, since ![]() , the
, the ![]() th derivative is just
th derivative is just ![]() .
.
So the series can be represented:
![]()
When ![]() :
:
![]()
series for ![]()
When ![]() etc.
etc.
The derivatives at ![]() are
are ![]() repeating endlessly.
repeating endlessly.
So the series is:
![]()
series for ![]()
When ![]() etc.
etc.
The derivatives at ![]() are
are ![]() repeating endlessly.
repeating endlessly.
So the series is:
![]()
(or simply differentiating the ![]() series term by term gets the same series.)
series term by term gets the same series.)
Euler’s identity
Substitute ![]() into the series for
into the series for ![]() to get:
to get:
![]()
Group the real and imaginary coefficients to get:
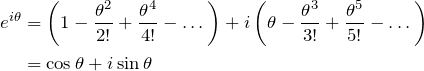
Plug in ![]() to get
to get ![]() , or
, or ![]() , “the most famous formula in all mathematics”.
, “the most famous formula in all mathematics”.
A poll of readers conducted by The Mathematical Intelligencer in 1990 named Euler’s identity as the “most beautiful theorem in mathematics”. In another poll of readers…by Physics World in 2004, Euler’s identity tied with Maxwell’s equations (of electromagnetism) as the “greatest equation ever”. – wikipedia
Great article here explaining its significance intuitively.
binomial expansion of ![]()
Proceeding as above,
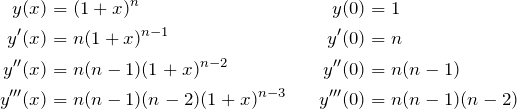
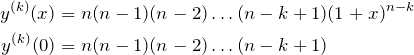
So the series can be written:
![Rendered by QuickLaTeX.com \begin{align*} (1+x)^n&=\sum^n_{k=0}\frac{y^{(k)}(0)}{k!}x^k\\ &=1+\frac{n}{1!}x+\frac{n(n-1)}{2!}x^2+\frac{n(n-1)(n-2)}{3!}x^3\\[8pt] &+\dots+\frac{n(n-1)(n-2)\dots (n-k+1)}{k!}x^k+\dots+\frac{n!}{n!}x^n \end{align*}](https://www.adamponting.com/wp-content/ql-cache/quicklatex.com-549d10474e1eddafb5dc5444374fa17e_l3.png)
The coefficient of ![]() is the binomial coefficient
is the binomial coefficient ![]() , also written
, also written ![]() :
:
![]()
Further reading
Hamming, Richard – Methods of Mathematics, ch20-21