Induction (under construction)
induction by the method of undetermined coefficients
Name and conquer
completing the square – see e.g. the quadratic formula
perturbation
If you have a transformation, look for an invariant!
Pigeonhole principle
Show that in any group of people, at least 2 will each know the same number of people.
Solution. With n people, label them according to how many they know. This will range from 0 to n-1. But If someone knows no-one (label 0), no-one knows n-1. By the pigeonhole principle, there are n people with n-1 labels, and at least 2 must know the same number of people.
Solution. With n people, label them according to how many they know. This will range from 0 to n-1. But If someone knows no-one (label 0), no-one knows n-1. By the pigeonhole principle, there are n people with n-1 labels, and at least 2 must know the same number of people.
Extremal principle: Pick an object which maximizes/minimizes some function.
Every member of Parliament has three enemies at most in the parliament. Show that one can divide the house into two groups so that every member has at most one enemy in his house.
Solution: Consider all partitions of the Parliament into two houses and, for each partition, count the total number E of enemies each member has in his house. The partition with minimal E has the required property. If some member had two or more enemies in his house, then he would have one enemy at most in the other house. By placing him in the other house, we could decrease the minimal E, which is a contradiction.
Solution: Consider all partitions of the Parliament into two houses and, for each partition, count the total number E of enemies each member has in his house. The partition with minimal E has the required property. If some member had two or more enemies in his house, then he would have one enemy at most in the other house. By placing him in the other house, we could decrease the minimal E, which is a contradiction.
divisibility
Sophie Germain’s identity:

Lagrange’s identity: ![]() .
.
Let 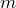 and
and 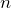 be distinct positive integers. Represent
be distinct positive integers. Represent 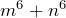 as the sum of two perfect squares different from
as the sum of two perfect squares different from 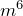 and
and 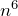 .
.
Solution: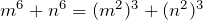
+++++++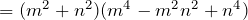
+++++++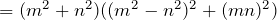
Substituting in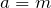 ,
, 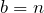 ,
, 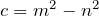 and
and 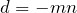 :
:
+++++++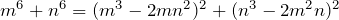 .
.
Solution:
Substituting in
Catalan’s identity
![]()
Proof: Set 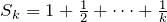
++++ 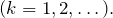 Then :
Then :
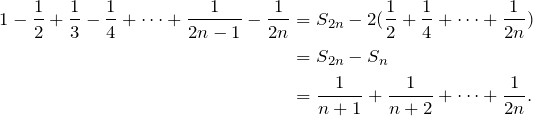
Search for a pattern.
Draw a figure.
Formulate an equivalent problem.
Modify the problem.

Choose effective notation.
Exploit symmetry.
Divide into cases.
Work backward.
Argue by contradiction.
Pursue parity.
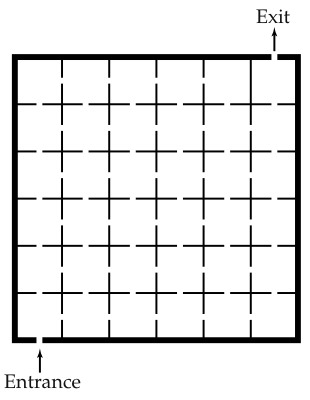 Q. In how many ways can you enter through one door, pass through every room exactly once, and go out the other door?
Q. In how many ways can you enter through one door, pass through every room exactly once, and go out the other door?
A. None. With this chess-board colouring, the 2nd, 4th and every even-numbered room visited is white. But there are an even number of rooms, and the last room on such a path would be even and black.
Generalize.
sources
Loren C Larson – Problem-solving through problems (1983)
Arthur Engel – Problem-solving Strategies (2008)