phinary

All numbers on this page are in phinary. i.e. base $\phi=\frac{\sqrt{5}+1}{2}$ .
$10$ = $\phi$ ,+ $0.1$ = $1/\phi$ .
Since $\phi^2=\phi+1$ , + $1=0.11=1/\phi+1/\phi^2=\frac{\phi+1}{\phi^2}=1.$

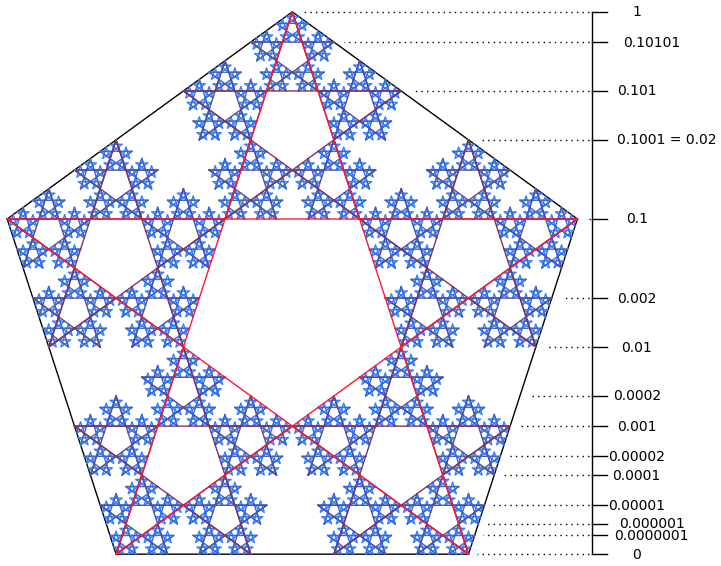
Measuring the (perpendicular) distance from each side in turn, anti-clockwise starting with the base, the coordinates for the top of the pentagon are $(1,0.1,0,0,0.1)$ . The coordinates of interior points add to $1.2=\sqrt{5}=0.221=10.1=2.001=1.022=0.31=0.132$ etc.
Since $\phi=\frac{\sqrt{5}+1}{2}$ , $\sqrt{5}=2\phi-1$ :
$\displaystyle 1.2=1+\frac{2}{\phi}=\frac{\phi+2}{\phi}=\frac{2(\phi+1)-\phi}{\phi}=\frac{2\phi^2-\phi}{\phi}=2\phi-1$ .
i.e. $\sqrt{5}=1.2=20-1$ .

The similarity of $1=0.11$ to the Fibonacci sequence rule $F_n=F_{n-1}+F_{n-2}$ isn’t a coincidence – the ratio of successive Fibonacci terms goes to $\phi$ as $n$ increases.