It seems there is a great confusion of terms in this area.
What is commonly called synthetic division is just one type of synthetic division, division of a polynomial by 
, for which it seems the best name is Ruffini’s rule.
Horner’s rule, or Horner’s form, is a polynomial in the form:
![\[(((a_n x+a_{n-1})x+a_{n-2})x+\dots+a_1)x+a_0\]](https://www.adamponting.com/wp-content/ql-cache/quicklatex.com-fc7c5518267d022194bb2bdd28335071_l3.png "Rendered by QuickLaTeX.com")
Horner’s method is a way of finding roots of a polynomial, by repeatedly reducing the equation by the integer part of a root, and multiplying the coefficients by factors of 10 to obtain further digits.
These are related but separate things.
E. J. Barbeau’s Polynomials – a problem book describes evaluating a polynomial by ‘constructing Horner’s table’ (i.e. plugging in e.g. 
to the Horner form) as ‘Horner’s method’. And then shows that this is an identical process to dividing the polynomial by 
. I suppose the confusion comes from these 2 procedures being identical. Although neither is apparently Horner’s method. He does division by polynomials of a higher degree with “Horner’s Method of Synthetic Division which can be regarded as a generalization of his method for division by a binomial 
“.
++++(He also adapts Horner’s table to convert powers and polynomials to falling (factorial) powers and polynomials – see below.)
Dividing a polynomial 
by 
with Ruffini’s rule either results in a remainder of 
, in which case 
is a root, or a remainder 
.
The polynomial remainder theorem states:
If a polynomial is divided by , then the remainder is a constant given by 
.
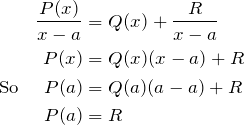
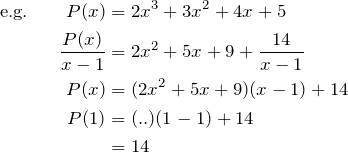
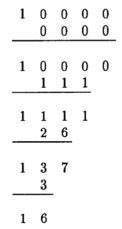
Barbeau’s table used to convert 
to falling powers:
references
Mathews, Walker – Mathematical Methods of Physics, 1971, p361-3