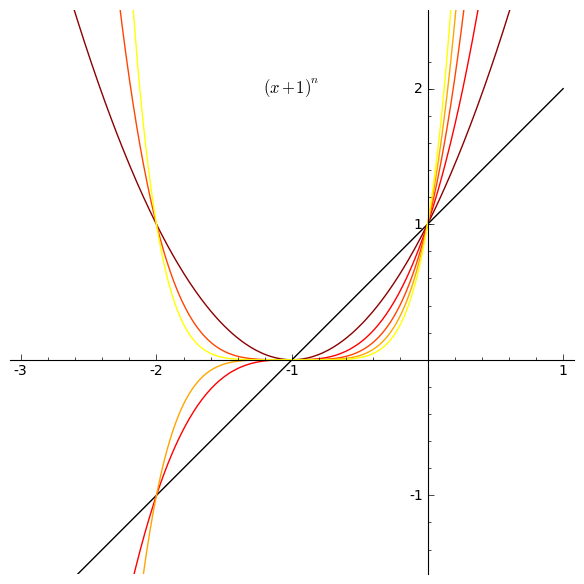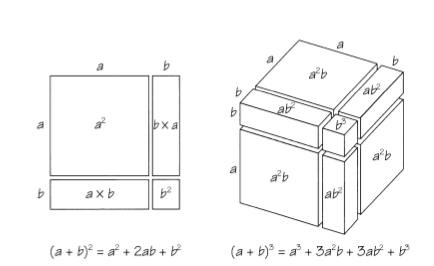
the binomial theorem

binom
The binomial theorem gives the values of the coefficients of the expansion of:

$\begin{align*} (a+b)^n&=(a+b)(a+b)(a+b)\dots(a+b)\\ \end{align*}$

where $n$ is any positive integer. (Newton gave the formula for any rational $n$ .)
The picture above shows the expansions for $n=2$ and $3$ .
The coefficients are the same as the rows of Pascal’s triangle.

$\displaystyle(a+b)(a+b)(a+b)\dots(a+b)$ is multiplied out by choosing one number from each bracket.
There is one way of choosing $a^n$ — choosing $a$ in each bracket, similarly one way of choosing $b^n$ .
There are $n$ ways of choosing $a^{n-1}b$ — one for each bracket the $b$ is chosen from.
These are combinations of $n$ elements, (in the strict mathematical sense of “combination”,) in which $\alpha$ identical elements $a$ and $\beta$ identical elements $b$ occur, where $\alpha+\beta=n$ .
The number of them is given by $\displaystyle C=\frac{n!}{\alpha!\beta!}$ .
( $0!$ is defined as $1$ , so that the formula gives the right answer for the number of occurrences of $\displaystyle a^n=\frac{n!}{n!0!}=1$ and $\displaystyle b^n=\frac{n!}{0!n!}=1$ .)

So now we have the binomial expansion:

$(a+b)^n=\sum_{\alpha+\beta=n} \frac{n!}{\alpha!\beta!} a^\alpha b^\beta$

For example,

$\begin{align*} (a+b)^5&=a^5+\frac{5!}{4!1!}a^4b+\frac{5!}{3!2!}a^3b^2+\frac{5!}{2!3!}a^2b^3+\frac{5!}{1!4!}ab^4+b^5\\[8pt] &=a^5+\frac{5\times4}{4}a^4b+\frac{5\times4}{2}a^3b^2+\frac{5\times4}{2}a^2b^3+\frac{5\times4}{4}ab^4+b^5\\[8pt] &=a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5\\ \end{align*}$

$\newline \newline$
$\displaystyle\frac{n!}{\alpha!\beta!}=\frac{n(n-1)(n-2)\dots(n-\alpha+1)}{1\cdot 2\cdot 3\dots \alpha}\quad$ is usually written $\displaystyle\quad\binom{n}{\alpha}$

$\binom{n+\beta}{\beta}=\frac{(\beta+1)(\beta+2)\dots(\beta+n)}{n!}=\binom{n+\beta}{n}$

Uh, or there’s Peter’s Method.

adamponting.com

the binomial theorem

Leave a Reply Cancel reply