[under construction]

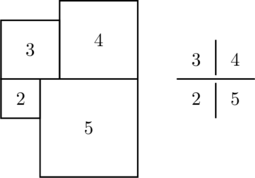
Mostly I’ll be working with h-lines, e.g. 3+4=2+5, a+b=c+d:

   

   

SQ TILINGS

Terminology

An h-line:

   

Mostly here we will be working with an adjacent h-line and v-line:

which I’ll call an hv-line, where , and , by definition.
A hv-line generates 4 arithmetic sequences, 2 going diagonally down to the right through a and b, and 2 going diagonally down to the left through b and e.
[do arrow notation, show example]
The minimum set of numbers to specify a complete tiling are:

a b | e
—-|
d |
– because , , and can usually be left off the notation.

To draw a tiling from this, extend the grid as far as needed, and fill in the blanks by extending the sequences, and completing h- and v-lines, then draw the squares. Negative and zero-sized squares fit without a problem.
(see page on how to do that)

Two layers

It seems that every tiling wraps around the plane twice – they are all double tilings – but only some have the same squares in the same positions in both layers.
Q. WHY????
The purpose of this study is to investigate and enumerate which of these 2-layer tilings have both layers the same, and thus can easily be drawn as tilings.
(Im not sure if some or all of the different-layered ones have layers containing a coincident seam, so the layers can be separated and drawn separately.)
*** tiling a different thing from the grid – every grid works fine, but only some tilings are same-layered.
conjecture: it’s when c=-f (in canonical form with d=0)
i.e. a+b=-(b-e)
b=(e-a)/2
i.e. (sticking with integers only) only when
e-a is even: a,e are both odd or both even.
[pic of centre of 8 1 | 10]
9 0 | -9
In the resulting tiling, 9 square is in the same place as the -9 square, and thus only when b=1 is it single-layered.
Q. when b=1+/-164n (i.e. multiples of A^2+B^2) what happens? Its on same map, but then c<>f.. It’s not the centre? hmm…. draw what happens.

Moving around the grid

Taking for a concrete example:

3 1 | 5
— |
4 0 |-4
and its associated grid.
[do drawing of adjacent squares so this is clear] … with the NE, NW etc hlines labelled as such.
The sequences to the upper left through a,d,e change by +3
to the upper right through a,d,e increase by +5
to the upper right through b,c,f decrease by 3 –> -3
to the upper left b,c,f increase by -> 5
Let’s label the 2 increments, calling 3, A, and 5, B.
Now let’s see what happens to the hline 3 1 as we move around the grid.
4 0
Moving north-west to the next h-line, [**add pic]
a and d increase by 3, b and c increase by 5, i.e.
it will be 3 1 + +A +B = 6 6
4 0 +B +A 9 3

Similarly, moving north-east:
[+B -A]
[-A +B]

Southwest:
[-B +A]
[+A -B]

Southeast:

[-A -B]
[-B -A]
Moving horizontally or vertically, or to any other h-line in the tiling, can be produced by a combination of these elementary operations.
e.g. horizontally to the right = Move SE+Move SW

Moving NE A times, produces:
[a+AB b-A^2]
[c-A^2 d+AB]

Moving SE B times produces:
[a-AB b-B^2]
[c-B^2 d-AB]
And doing these 2 groups consecutively produces:
[a b-(A^2+B^2)]
[c-(A^2+B^2) d]
i.e. you can add +/-(A^2+B^2) to b and c any number of times and stay on the same tiling.

Canonical form

A hv-line can always be reduced to the form
A | B
0 |

where

*SHOW HOW
Starting with any h-line..
-Divide through by any common denominator in a,b,d,e
-Draw the extended h-line (9 squares) and choose a,d,e so a,e>=d and a>=3
(perhaps sideways, upside down etc from the extended h-line)
-add/subtract A and B to a,d,e to make d=0
– add +/-(A^2+B^2) to b,c so that b,c are the smallest obtainable values both >=0.

Same-Layered tilings

Q. For any A and B, which b produces a single tiling? (both layers the same)

1. A and B both odd
5 x | 7
0 |
works with x=-36,1 and 38, and no other values between.
i.e. -(A^2+B^2)/2+1, 1 and (A^2+B^2)/2+1
*NB is it that? or -AB-1 and AB+3?! investigate.
a. “1” works because then c=6 and f=-6 and those squares occupy the same exact location.
b. the others.. are what? why (A^2+B^2)>>>/2<<< ? because its an integer?.. uh,,, --> If A^2+B^2 is even, then x+(A^2+B^2)/2 and x-(A^2+B^2)/2 will be on a tiling the same as x but upside-down (rotated 180 degrees).
(The same thing happens with an odd A^2+B^2, only then b,c,f are fractions /2 – multiply everything by 2 for an integer-sided tiling the same shape.)

2. A and B odd+even
4 x | 5
0
works with x=-20 or 21.
So one expects it will work with x=0.5, i.e. multiplying through by 2:
8 1 | 10
0
-which is an example of
3. A and B both even

Q. So, what is the canonical form for the P. packings?
and
Q. Which of them are single-layered?