THE DISSECTION OF RECTANGLES INTO SQUARES – Brooks, Smith, Stone, Tutte 1940
SQUARING THE SQUARE – Tutte 1948
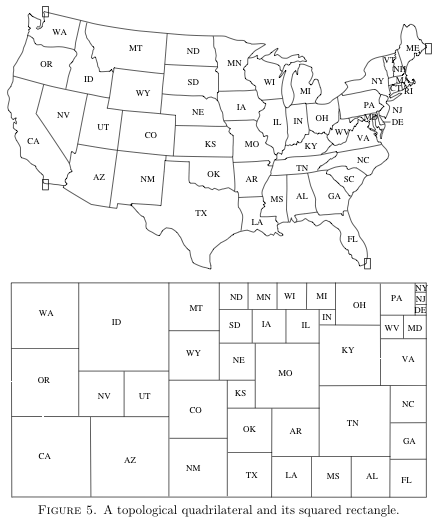
SQUARING RECTANGLES: THE FINITE RIEMANN MAPPING THEOREM – Cannon, Floyd, Parry 1991 mageps.pdf
ABSTRACT. The classical Riemann mapping theorem asserts that any topological quadrilateral in the complex plane can be mapped conformally onto a rectangle. The finite Riemann mapping theorem asserts that any topological quadrilateral tiled by finitely many 2-cells can be mapped with minimal combinatorial distortion onto a rectangle tiled by squares. We prove the finite Riemann mapping theorem, discuss its connections with the classical theories of conformal mapping and electric circuits, and develop algorithms for calculating the finite Riemann mapping.
SQUARE TILINGS WITH PRESCRIBED COMBINATORICS – Oded Schramm 1993
Packings. Square tilings. Extremal length. Discrete extremal length. Duality. The algorithm. Extremal length in arbitrary graphs.
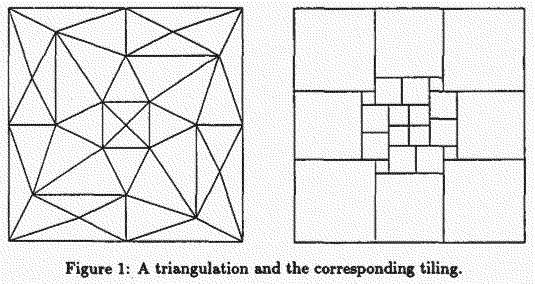
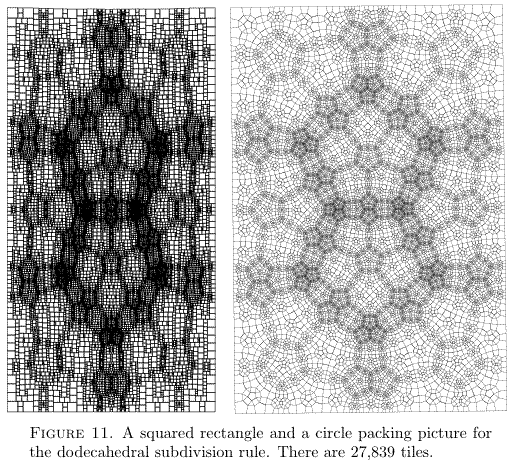
THE LENGTH-AREA METHOD AND DISCRETE RIEMANN MAPPINGS – Cannon, Floyd, Parry 1999
lamdrm.pdf
1. The length-area method 2. 3-manifold groups 3. The Riemann mapping theorem 4. The combinatorial Riemann mapping theorem 5. How should we view examples? (i.e. using squares or lines from circle packing?)
Conformal modulus: the graph paper invariant or The conformal shape of an algorithm – Cannon, Floyd, Parry 1999 conshape.pdf
“What is the geometry underlying the modulus formula,
![\[M_\rho = (H_\rho)^2 /A_\rho,\]](https://www.adamponting.com/wp-content/ql-cache/quicklatex.com-0c97ae4b48ee3f26f01c76162950cdb4_l3.png "Rendered by QuickLaTeX.com")
which comes from the theory of conformal mapping and gives the modulus 
as a ratio which compares the square 
of a certain length 
to an area 
? Just as Dr. Strangelove came to love the bomb, so we have come to love this unintuitive expression. Our aim is to explain to topologists and geometric group theorists its beautiful underlying geometry and applications.”
SQUARING RECTANGLES FOR DUMBBELLS – Cannon, Floyd, Parry 2008
ABSTRACT. The theorem on squaring a rectangle (see Schramm 1993 and Cannon-Floyd-Parry 1991) gives a combinatorial version of the Riemann mapping theorem. We elucidate by example (the dumbbell) some of the limitations of rectangle-squaring as an approximation to the classical Riemann mapping.
Slides from a 1997 talk by James Cannon
