A symmetric function of ![]() is one whose value is unchanged if
is one whose value is unchanged if ![]() are permuted arbitrarily. For example, each of the following is a symmetric function of three variables:
are permuted arbitrarily. For example, each of the following is a symmetric function of three variables:
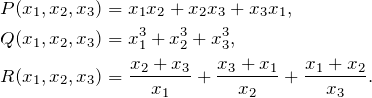
Certain symmetric functions serve as building blocks for all the rest. Let
![]()
where the sum is taken over all ![]() choices of the indices
choices of the indices ![]() from
from ![]() .
.
Then ![]() is called the
is called the ![]() th elementary symmetric function of
th elementary symmetric function of ![]() .
.
Every symmetric polynomial function of ![]() is a polynomial function of
is a polynomial function of ![]() . (And every rational function of
. (And every rational function of ![]() is a rational function of
is a rational function of ![]() .)
.)
E.g. For ![]() the elementary symmetric functions are
the elementary symmetric functions are
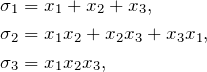
and the above examples expressed in terms of these are:
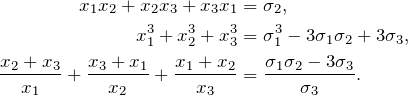
![]()
and let ![]() be the
be the ![]() th elementary symmetric function of the
th elementary symmetric function of the ![]() . Then
. Then
![]()
Explanation. On the LHS of the equation
![]()
the coefficient of ![]() is
is ![]() ; on the RHS, the coefficient of
; on the RHS, the coefficient of ![]() is
is ![]() times the sum of all
times the sum of all ![]() products of
products of ![]() of the
of the ![]() . Thus
. Thus ![]() .
.
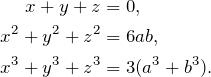
Solution. The LHS of each equation is a symmetric function of ![]() ,
, ![]() ,
, ![]() . This suggests that we can use the information given to construct a polynomial equation whose roots are
. This suggests that we can use the information given to construct a polynomial equation whose roots are ![]() ,
, ![]() ,
, ![]() . Let
. Let
![]()
Then ![]() and
and
![]()
Finally, ![]() yields
yields
![]()
from which we find
![]()
Thus ![]() ,
, ![]() ,
, ![]() are the roots of the cubic equation
are the roots of the cubic equation
![]()
Observe that ![]() is one of the roots. Now we can factor to obtain
is one of the roots. Now we can factor to obtain
![]()
and so find the complete solution set:
![]()
where ![]() and
and ![]() are the two complex cube roots of
are the two complex cube roots of ![]() .
.
source
Lozansky, Rousseau – Winning Solutions (1996)