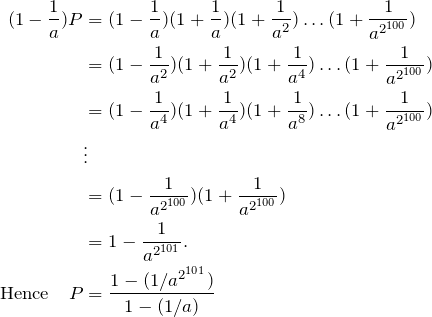the “catalyst” tool
Utilizing difference-of-squares in telescoping products that are geometric series.
Example. Simplify the product
![]()
Call this ![]() , and multiply it by the catalyst
, and multiply it by the catalyst ![]() .
.
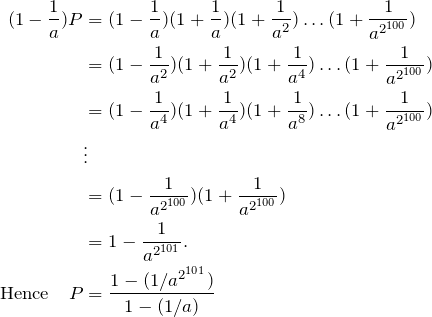
the “catalyst” tool
Utilizing difference-of-squares in telescoping products that are geometric series.
Example. Simplify the product
![]()
Call this ![]() , and multiply it by the catalyst
, and multiply it by the catalyst ![]() .
.