For positive numbers ![]() and
and ![]() , the geometric mean is
, the geometric mean is ![]() .
.
e.g. If an investment earns 25% in the first year (i.e. the amount is multiplied by ![]() ) and 80% in the second year (
) and 80% in the second year (![]() ) then the average annual rate of return
) then the average annual rate of return ![]() is
is ![]() , since
, since ![]() .
.
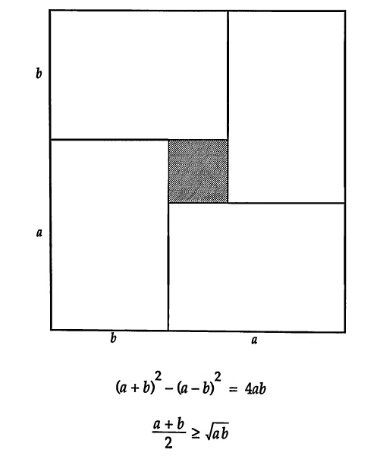
For positive ![]() ,
, ![]()
The two sides are equal when ![]()
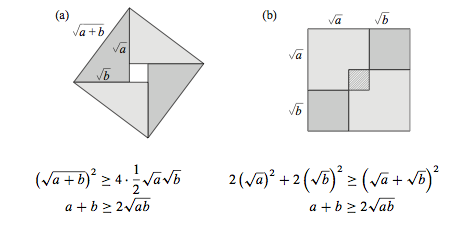
For ![]() :
:
![]()
as shown in the following diagrams:
1.
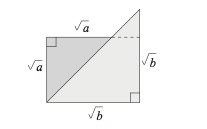
i.e. when ![]() , the rectangle
, the rectangle ![]() is smaller than the area of the two triangular half-squares
is smaller than the area of the two triangular half-squares ![]()
2.
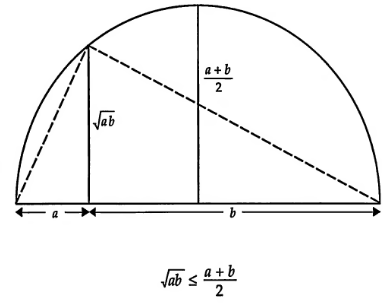
Why is the height ![]() ?
?
By similar triangles, ![]()
![]()
Harmonic mean
If we travel a distance ![]() at rate
at rate ![]() in time
in time ![]() and make the return trip at rate
and make the return trip at rate ![]() in time
in time ![]() , then
, then ![]() . What’s the average rate for the full trip?
. What’s the average rate for the full trip?
![]() and therefore:
and therefore:
![Rendered by QuickLaTeX.com \[r=\frac{2d}{t_1+t_2}=\frac{2d}{\frac{d}{r_1}+\frac{d}{r_2}}=\frac{2r_1r_2}{r_1+r_2}\]](https://www.adamponting.com/wp-content/ql-cache/quicklatex.com-2d3818e6b5f756e97e0665e769536847_l3.png)
This average rate is the harmonic mean of the two rates, and less than the average – the arithmetic mean ![]() – when the rates differ, because more time is spent at the lower speed.
– when the rates differ, because more time is spent at the lower speed.
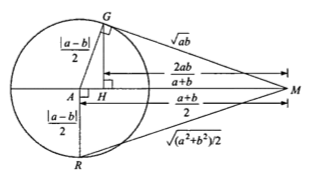
HM 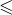 GM
GM 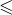 AM
AM
i.e. ![]() .
.
Some other means
Root mean square (RMS) :+++ ![]()
Contraharmonic mean :+++ ![]()
Heronian mean :+++ ![]()
Logarithmic mean :+++ ![]()
Identric mean :+++ ![]()
References
Alsina, Nelsen – When Less Is More
Nelsen – Proofs Without Words, I & II