2D
Looking first at the jigsaw method in 2D: eg with 200/117.

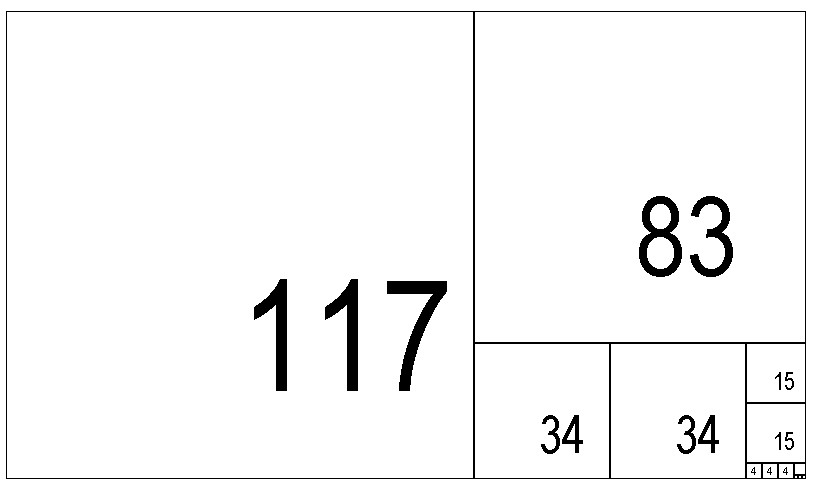
This rectangle, when filled with the biggest squares possible, gives 1, 1, 2, 2, 3, 1, 3 of each size rectangle, giving the continued fraction [1;1,2,2,3,1,3], i.e.

   

This led me to wondering whether a 3D version of this would work.

differences between 2D and 3D and making conventions for 3D

The “1/” in the 2D continued fraction means just “change angle of view by ” – seen horizontally (x axis) is seen vertically (y axis).
In 3D there are 3 orthogonal directions, obviously, but as long as they are always rotated in the same order, this should work, i.e. be unambiguous and avoid “noncanonicity”. So “1/” in 3D, let’s say, means change angle by , in the order .
Cubes in 3D are represented by integers. As in the 2D version, (for the continued fraction at least), the size doesn’t matter, just the number of them – the number of times the denominator goes into the numerator = the floor function of the fraction, e.g. with 13/2 or 601/100 it equals 6.
But we can’t just fill a 3D box with cubes, usually – except if the ratio is an integer. In 3D there are two sides to be aligned with, not just 1 as in 2D. But flattened cubes – square prisms e.g. a 5x5x3 box, will suffice. I’m not sure how to conceptualize a square prism like 5x5x3 as a number. A complex one, I guess, a vector, a matrix…
The convention is, the first number gives the length in whatever direction we’re looking. 6x3x3 would be two cubes, i.e. 6x3x3=2. Nothing is lost here – the shape of 6x3x3 just is 2, i.e. 2 cubes next to each other. (Like with 2D, the ratio between the numbers is what is important, not the their absolute size.) Viewed from away, in either of the 2 other directions, it = 1/2.
So since 3x3x3=1, I suppose 5x3x3 should be 5/3. But in any case, the square prisms used will usually be seen side on, e.g. 5x5x3. The side in the direction of sight will be at least as long as either of the other sides, but usually the longest two sides will be equal. Thus 5x5x3 can be represented 5×3, which will always mean a 5x5x3 square prism, viewed in the direction of the first 5.
OK, some examples!

17x12x8

19x14x11
3 pretty randomly chosen relatively prime numbers.

8x8x3

8x3x3

x1x1

xx1

a fibonacci analogue

finding an analogue of
Is there an analogue of the 2D ?
This equation would mean in 3D: Some box, when a cube is put next to it, viewed from , is the same shape as original box.
If the cube is a x a x a units, the box would have to have two sides of a for the cube to fit against. The third side, b, must be much smaller if this is possible. so a x a x b must be the same shape as (b+a) x a x a (the box and cube together). This is not at all possible. If b is smaller than a, it cannot be similar to the box + cube, as that has its two smaller sides equal. If bigger, it must = b + a. But then b=b+a, again impossible.

How about adding another layer, 3 changes of angle for the 3 dimensions. Sounds more promising. So then try x = a x b x c +
That would mean: a box with a cube put next to it, with another box put on top. These 3 together are the same shape as the first box.

what is it good for?! does it find the 3D gcd or something?

convergents of the 3D continued fraction

other thoughts

If the absolute magnitude doesnt matter, why not normalize every box to axbx1? (i.e. axbx1, axax1 or ax1x1)
why not. I guess because then we won’t usually/always get integer side lengths. Maybe when there are irrational side lengths, this could be possible/better… to simplify things.