Euler’s phi function 
, or totient, counts how many positive integers lower than 
have no common divisor with .
The 
function was first studied by Euler, though it was Gauss who named it and established that, for any positive integer n,
(1) 
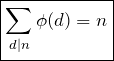
where the summation is over all positive divisors d of n.
= 
when 
. (Euler 1761)
is also naturally the number of proper fractions in lowest terms with denominator 
. e.g. for 
, there are 
, 
and 
.