Given two real numbers ![]() and
and ![]() , if
, if ![]() is their sum and
is their sum and ![]() their product,
their product, ![]() and
and ![]() are:
are:
![]()
This is basically the quadratic formula – note that ![]() .
.
Derivation using quadratic formula
![]() and
and ![]() , so:
, so:
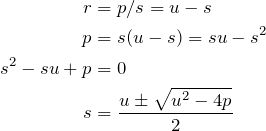
Since ![]() and
and ![]() are symmetrical in
are symmetrical in ![]() and
and ![]() , the same equation gives
, the same equation gives ![]() .
.
Graphical derivation
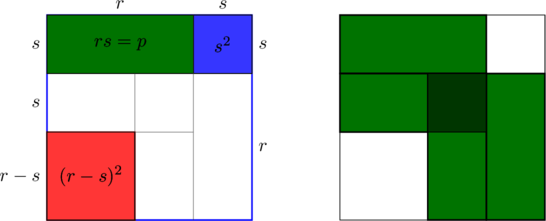
The difference in area between the red square ![]() and the largest square
and the largest square ![]() is evidently equal to 4 of the green rectangles each of area
is evidently equal to 4 of the green rectangles each of area ![]() . (See in the right picture that the dark green overlap
. (See in the right picture that the dark green overlap ![]() is equal in area to the square at top right not covered.)
is equal in area to the square at top right not covered.)
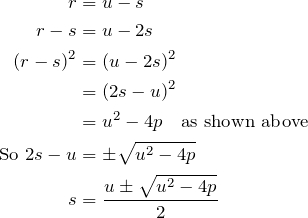
Since similarly ![]() , and
, and ![]() , the RHS also gives
, the RHS also gives ![]() .
.

Pic from E. Hairer and G. Wanner, Analysis by its History, 2008.
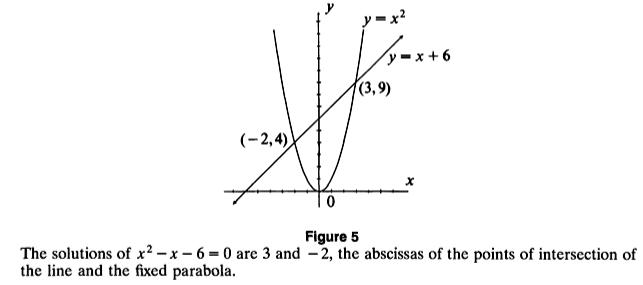
Graph of ![]() and
and ![]() :
: