generating functions

The basic generating function has the form:

$\boxed{G(z) = g_0+g_1 z+g_2 z^2 +g_3 z^3 +g_4 z^4 + \dotsb = \sumzn{g_n}}$

$G(z)$ , or $G$ for short, is the generating function for the sequence $\seqd{g_0,g_1,g_2}$ , also called $\angb{g_n}$ . The coefficient $g_n$ of $z^n$ in $G$ is denoted $[z^n]G(z)$ .

There are two kinds of “closed form” in generatingfunctionology.

a closed form for 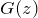$G(z)$ , expressed in terms of $z$ , and
a closed form for 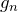$g_n$ , expressed in terms of $n$ .

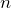e.g. the generating function for Fibonacci numbers has the closed form $z/(1-z-z^2)$ ; the Fibonacci numbers themselves have the closed form $(\phi^n-\hat{\phi}^n)/\sqrt{5}$ .

Solving recurrences – THE METHOD

Given a sequence $\angb{g_n}$ that satisfies a given recurrence, we seek a closed form for $g_n$ in terms of $n$ . A solution to this problem via generating functions proceeds in four steps:

Write down a single equation that expresses 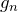$g_n$ in terms of other elements of the sequence. This equation should be valid for all integers 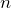$n$ , assuming that $g_{{}^\_1}=g_{{}^\_2}=\dotsb=0$ .
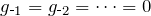Multiply both sides of the equation by 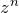$z^n$ and sum over all 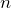$n$ . This gives, on the left, the sum 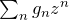$\sum_n g_n z^n$ , which is the generating function 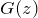$G(z)$ . The right-hand side should be manipulated so that it becomes some other expression involving $G(z)$ .
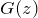Solve the resulting equation, getting a closed form for $G(z)$ .
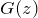To find an exact formula, a closed form for the sequence:
- Expand 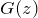$G(z)$ into a power series and read off the coefficient of $z^n$ .
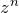- If G is a rational function (quotient of two polynomials)
  - expand in partial fractions and handle the terms separately.
  - OR: If the roots of the denominator polynomial are all different, use the rational expansion theorem below.

The “routine stunt”

$\boxed{\sumn nx^n = \sumn x (\ddx) x^n = x (\ddx) \sumn x^n = x (\ddx) \fr{1-x}=\frac{x}{(1-x)^2}}$

Expanding partial fractions
e.g. Expand $A(x) = \dfrac{1-2x+2x^2}{(1-x)^2(1-2x)}.$
This will be expandable in the form $\dfrac{A}{(1-x)^2}+\dfrac{B}{1-x}+\dfrac{C}{1-2x}$ .
To find $A$ , multiply both sides by $(1-x)^2$ and let $x=1$ . $\To A=-1$
To find $C$ , multiply both sides by $1-2x$ and let $x=1/2$ . $\To C=2$
To find $B$ , substitute in $x=0$ and use the values of $A$ and $C$ to find $B$ . $\To B=0$
So $A(x)= \dfrac{-1}{(1-x)^2}+ \dfrac{2}{1-2x}$

Rational expansion theorem for distinct roots

If $R(z)=P(z)/Q(z)$ , where $Q(z)=q_0(1-\rho_1 z)\dots(1-\rho_m z)$ and the roots $(\rho_1,\dots,\rho_m)$ are distinct, and if $P(z)$ is a polynomial of degree less than $m$ , then

$\boxed{[z^n] R(z)=a_1\rho_1^n+\dotsb+a_m\rho_m^n \text{, where } a_k=\frac{-\rho_k P(1/\rho_k)}{Q'(1/\rho_k)}}$

i.e.

$\boxed{[z^n] R(z)=\sum_{k=1}^m \frac{-\rho_k^{n+1} P(1/\rho_k)}{Q'(1/\rho_k)}}$

When $Q(z)$ is quadratic, i.e. $m=2$ , the equation becomes

$\boxed{[z^n] R(z) = -\rho_1^{n+1}\frac{P(1/\rho_1)}{Q'(1/\rho_1)}-\rho_2^{n+1}\frac{P(1/\rho_2)}{Q'(1/\rho_2)}}$

Basic generating function manipulations

$\begin{align*} \alpha F(z)+\beta G(z) &= \sum_{n}(\alpha f_n+\beta g_n)z^n\\ z^m G(z) &= \sum_n g_{n-m} z^n, \text{ integer } m\ges 0\\ \frac{G(z)-g_0-g_1 z-\dotsb -g_{m-1}z^{m-1}}{z^m} &= \sumzn{g_{n+m}}, \text{ integer } m\ges 0\\ G(cz) &= \sum_n c^n g_n z^n\\ G'(z) &= \sum_n (n+1)g_{n+1}z^n\\ zG'(z) &= \sum_n n g_n z^n\\ \int_0^z G(t) \,\mathrm{d}t &= \snge{1} \fr{n}g_{n-1}z^n\\ F(z)G(z) &= \sum_n \left(\sum_k f_k g_{n-k}\right)z^n\\ \fr{1-z}G(z) &= \sum_n\left(\sum_{k \les n} g_k\right)z^n\\ \end{align*}$

The calculus of ordinary power series generating functions

Definition. The symbol $f \ops \anzi$ means that the series $f$ is the ordinary power series (‘ops’) generating function for the sequence $\anzi$ , i.e. $f=\sum_n a_n z^n$ .

Shifting the subscript by 1. $\To$ the series changes by difference quotient $(f-a_0)/x$

$\sumzn{a_{n+1}} = \fr{z} \sum_{m \ges 1} a_m z^m = \frac{f(z)-f(0)}{z}.$

Therefore $f \ops \anzi \To \dfrac{f-a_0}{z} \ops \azi{n+1}.$
Shift subscript by 2 $\To$ Iterate the difference quotient operation.

$\azi{n+2} \ops \frac{\big((f-a_0)/z\big)-a}{z} = \frac{f-a_0-a_1z}{z^2}.$

e.g. the Fibonacci recurrence relation $F_{n+2}=F_{n+1}+F_n$ $(n \ges 0,F_0=0,F_1=1)$ translates directly into $\dfrac{f-x}{x^2}=\dfrac{f}{x}+f$ .

Rule 1. Shifting subscript. If $f \ops \anzi$ , then, for integer $h \geq 0$ ,

$\boxed{\azi{n+h} \ops \frac{f-a_0-a_1z-\dotsb-a_{h-1}z^{h-1}}{z^h}}$

Multiplying terms by $n$ and its powers. $\sum_n n a_n x^n=xf'.$ To multiply the $n$ th member of a sequence by $n$ causes its ops generating function to be multiplied by $x(\ddx)$ , which we will write as $xD$ . i.e.

$f \ops \anzi \To (xDf) \ops \zi{na_n}.$

What generates $\zi{n^2a_n}$ ? $(xD)^2f$ . In general,

$(xD)^kf \ops \{n^ka_n\}_{n \ges 0}.$

What generates $\{(3-7n^2)a_n\}_{n \ges 0}$ ?
Do the same thing to $xD$ that is done to $n$ : $(3-7(xD)^2)f$ .

Rule 2. If $f \ops \anzi$ , and P is a polynomial,

$\boxed{P(xD)f \ops \{P(n)a^n\}_{n \ges 0}.}$

Examples.
Find $= \sum_{n \ges 0} (n^2+4n+5)/n!$ (The terms are $5,10,\frac{17}{2},\frac{13}{3},\frac{37}{24},\frac{5}{12}\dots$ )
The answer is the value at $x=1$ of the power series (ignoring convergence issues).

$\begin{align*} \{(xD)^2+4(xD)+5\}e^x&=\{x^2+x\}e^x+4xe^x+5e^x\\ &=(x^2+5x+5)e^x\\ &=11e.\\ \end{align*}$

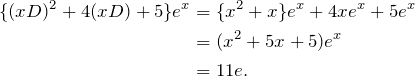
Find a closed formula for the sum of the squares of the first N positive integers.
Begin with the fact that $\sum_{n=0}^N x^n=\dfrac{x^{N+1}-1}{x-1}$ . To obtain the desired series, apply $(xD)^2$ to both sides, then set $x=1$ .

$\begin{align*} \sum_{n=1}^N n^2 &= (xD)^2 \left\{ \frac{x^{N+1}-1}{x-1} \right\} \text{ when } x=1.\\ &=\text{..then a miracle occurs..}\\ &=\frac{N(N+1)(2N+1)}{6} \end{align*}$

Rule 3. Multiplication of two gfs. If $f \ops \anzi$ and $g \ops \zi{b_n}$ , then

$\boxed{fg \ops \left\{\sum_{r=0}^n a_r b_{n-r} \right\}_{n=0}^\infty }$

If $f,g,h$ are three series that generate sequences $a,b$ and $c$ ,

$fgh \ops \left\{\sum_{r+s+t=n} a_r b_s c_t \right\}_{n=0}^\infty$

Rule 4. Powers of a series. If $f \ops \anzi$ , then for a positive integer $k$ ,

$\boxed{ f^k \ops \left\{ \sum_{n_1+n_2+\dotsb+n_k=n} a_{n_1}a_{n_2}\dotsb a_{n_k} \right\}_{n=0}^\infty }$

Example. Find $f(n,k)$ , the number of ways a nonnegative integer $n$ can be written as an ordered sum of $k$ nonnegative integers.
e.g. $f(4,2)=5$ , because $4=4+0=3+1=2+2=1+3=0+4$ .
Consider the power series $1/(1-x)^k$ . Since $1/(1-x) \ops \{1\}$ , by Rule 4 we have

$1/(1-x)^k \ops \{ f(n,k)\}_{n=0}^\infty$

Since $\sum_k \binom{n}{k} x^k =(1+x)^n$ , $f(n,k)=\binom{n+k-1}{n}$ .

If $f \ops \anzi$ , what sequence does $\dfrac{f(x)}{1-x}$ generate?

$\begin{align*} \frac{f(x)}{1-x}&=(a_0+a_1x+a_2x^2+\dotsb)(1+x+x^2+\dotsb)\\ &=a_0+(a_0+a_1)x+(a_0+a_1+a_2)x^2+(a_0+a_1+a_2+a_3)x^3+\dotsb \end{align*}$

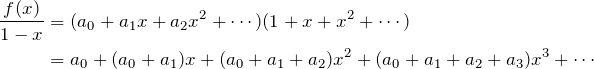
Rule 5. Dividing by $1-x$ . If $f \ops \anzi$ then

$\boxed{\frac{f}{1-x} \ops \left\{ \sum_{j=0}^n a_j\right\}_{n \ges 0}}$

i.e. dividing by $1-x$ replaces the generated sequence by the sequence of its partial sums.

bibliography

Concrete Mathematics – Knuth, Graham, Patashnik, 2nd Ed., Ch. 7
generatingfunctionology – Herbert Wilf – read online

adamponting.com

generating functions

Leave a Reply Cancel reply