(unfinished)
![]() is some irrational number, with a weird decimal going on forever. With this method you can calculate it as exactly as you want, or the square root of any number, without having any idea what it is! Well, knowing only that it’s between 3 and 4. because
is some irrational number, with a weird decimal going on forever. With this method you can calculate it as exactly as you want, or the square root of any number, without having any idea what it is! Well, knowing only that it’s between 3 and 4. because ![]() and
and ![]() is 16, so it’s somewhere in there.
is 16, so it’s somewhere in there.
The only slightly tricky thing in this method is knowing (i.e. remembering from high school) how to get the ![]() from the bottom to the top of a fraction, so read the short explanation of how to do that using conjugate surds if you need to.
from the bottom to the top of a fraction, so read the short explanation of how to do that using conjugate surds if you need to.
OK, let’s begin…
We are going to make a continued fraction for ![]() , which may then be used to make rational approximations of any desired accuracy. (And convergents (fractions) made from continued fractions are the most accurate fractional approximations for their size.)
, which may then be used to make rational approximations of any desired accuracy. (And convergents (fractions) made from continued fractions are the most accurate fractional approximations for their size.)
We will be finding ![]() , and the integers making up the continued fraction
, and the integers making up the continued fraction ![]()
Firstly, set ![]() .
.
The algorithm has only two steps, repeated ad nauseam:
Step 1. Set ![]()
This is the ‘floor’ function, meaning round it down to the nearest integer. Which is lucky, cause that’s all I know about ![]() !
!
Step 2. ![]()
Then repeat…
Ok, round 1.
1. ![]() .
.
2. ![]()
That was easy. Round 2*..
1. ![]() – and here’s the tricky bit I spoke of earlier, multiplying by the conjugate surd to make it much easier to deal with.
– and here’s the tricky bit I spoke of earlier, multiplying by the conjugate surd to make it much easier to deal with.
Hey, we’ve already done this step. ![]()
So ![]() The
The ![]() is rounded down to
is rounded down to ![]() again.
again.
And ![]() is rounded down to
is rounded down to ![]() . So
. So ![]()
2. 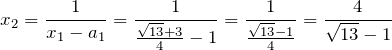
Round 3.
1. ![]()
First multiply by the conjugate as always. ![]()
2. ![]()
Round 4.
1. ![]()
![]()
2. ![]()
To be continued!
*Yes, this is a boxing metaphor. Weird, huh.
(Method stolen from Koshy’s Elementary Number Theory with Applications, 2007 – it’s just Euclid’s algorithm really.)