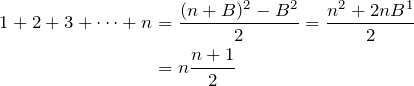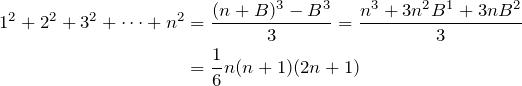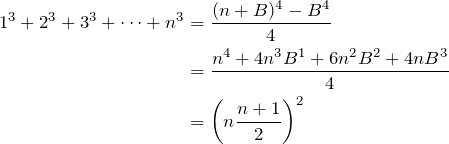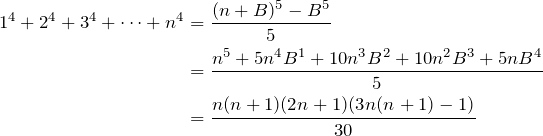For any positive integer ![]() , find
, find
![]()
“The following elegant solution [says Dörrie] is based upon the binomial theorem.
By resorting to the device of considering the magnitudes ![]() resulting from the binomial expansion of
resulting from the binomial expansion of ![]() as unknowns subject to
as unknowns subject to ![]() certain conditions rather than as powers of
certain conditions rather than as powers of ![]() , we obtain an amazingly short derivation of
, we obtain an amazingly short derivation of ![]() .”
.”
(This type of crazy-looking procedure is Blissard’s symbolic method, or umbral calculus, introduced by John Blissard in 1861. Also used extensively by Lucas. Now referred to as 19th C or classic umbral calculus, as since the 1970s the subject has been transformed by Roman, Rota and others.)
According to the binomial theorem, if ![]() ,
,
![]()
and
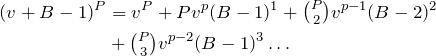
Since ![]() subtracting the second equation from the first gives:
subtracting the second equation from the first gives:
![Rendered by QuickLaTeX.com \begin{align*} \mathrm{(I)} \qquad (v+B)^P-(v+B-1)^P&=Pv^p+\tbinom{P}{2}v^{p-1}[B^2-(B-2)^2]\\ &+\tbinom{P}{3}v^{p-2}[B^3-(B-1)^3]\dots \end{align*}](https://www.adamponting.com/wp-content/ql-cache/quicklatex.com-572a3aa5c58ee1189f12764326ebdf97_l3.png)
Now define the unknowns ![]() by the equations
by the equations
![]() etc.
etc.
This simplifies ![]() to
to
![]()
Substitute in ![]() to get
to get

Addition of these ![]() equations gives
equations gives
![]()
or
![]()
Now to determine ![]() from equations
from equations ![]() ,
, ![]() ,
, ![]()
From ![]() it follows that
it follows that ![]()
From ![]() ,
, ![]()
From ![]() ,
, ![]()
![]()
From ![]() ,
, ![]()
These are known as the Bernoulli numbers:
![]()
Then from ![]() we get
we get