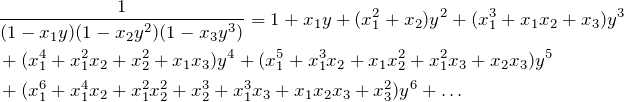![]()
Some simple sequences and their generating functions
![Rendered by QuickLaTeX.com \begin{align*} &\mathsf{sequence} &&\mathsf{gen.\; function} &&\mathsf{closed\; form}\\ &\seqd{1,0,0,0,0,0} &&\sumzn{[n=0]} &&1\\ &\seqd{0,\dots,0,1,0,0} &&\sumzn{[n=m]} &&z^m \\ &\seqd{1,1,1,1,1,1} &&\sumzn{} && \fr{1-z}\\ &\seqd{1,-1,1,-1,1,-1} &&\sumzn{(-1)^n} && \fr{1+z}\\ &\seqd{1,0,1,0,1,0} &&\sumzn{[2\backslash n]} && \fr{1-z^2}\\\ &\seqd{1,0,\dots,0,1,0,\dots,0,1,0} &&\sumzn{[m\backslash n]} && \fr{1-z^m}\\ &\seqd{1,2,3,4,5,6} &&\sumzn{(n+1)} && \fr{(1-z)^2}\\ &\text{Triangular numbers}&& && \\ &\seqd{1,3,6,10,15,21} &&\sumzn{\binom{n+2}{2}} && \fr{(1-z)^3}\\ &\text{Tetrahedral numbers}&& && \\ &\seqd{1,4,10,20,35} &&\sumzn{\binom{n+3}{3}} && \fr{(1-z)^4}\\ &\seqd{1,5,15,35,70} &&\sumzn{\binom{n+4}{4}} && \fr{(1-z)^5}\\ &\textstyle\seqd{1,c,\binom{c+1}{2}, \binom{c+2}{3}} &&\displaystyle\sumzn{\binom{c+n-1}{n}} && \fr{(1-z)^c}\\ &\text{equivalent to} &&\sumzn{\binom{n+k}{k}} && \fr{(1-z)^{k+1}}\\ \end{align*}](https://www.adamponting.com/wp-content/ql-cache/quicklatex.com-8401ff63180e325c1606874e78e444e3_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} &\seqd{0,1,4,9,16} &&\sumzn{n^2} && \frac{z(z+1)}{(1-z)^3}\\ &\seqd{1,2,4,8,16,32} &&\sumzn{2^n} && \fr{1-2z}\\ &\seqd{1,4,6,4,1,0,0} &&\sumzn{ \binom{4}{n}} && (1+z)^4\\ &\textstyle\seqd{1,c,\binom{c}{2}, \binom{c}{3}} &&\sumzn{\binom{c}{n}} && (1+z)^c\\ &\seqd{1,c,c^2,c^3} &&\sumzn{c^n}&& \fr{1-cz}\\ &\seqd{0,1,\fr{2},\fr{3},\fr{4}} &&\snge[1] \fr{n}z^n && \ln\fr{1-z}\\ &\langle 0,1,-\fr{2},\fr{3},-\fr{4},\dots\rangle &&\snge[1] \frac{-1^{n+1}}{n}z^n && \ln (1+z) \\ &\langle 1,1,\fr{2},\fr{6},\fr{24},\fr{120},\dots\rangle &&\sumzn{\frac{1}{n!}} && e^z\\ &\seqd{0,1,0,\fr{3!},0,\fr{5!}} && \sumzn{\fr{n!}[2\backslash (n+1)]} && \sin{z}\\ &\seqd{1,0,\fr{2!},0,\fr{4!},0} && \sumzn{\fr{n!}[2\backslash (n+2)]} && \cos{z}\\ &\seqd{} && \sumzn{} && \\ \end{align*}](https://www.adamponting.com/wp-content/ql-cache/quicklatex.com-225ed61a2a84eb08c1f2d2b185c69951_l3.png)
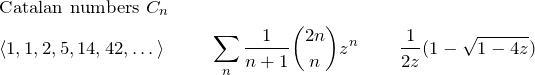
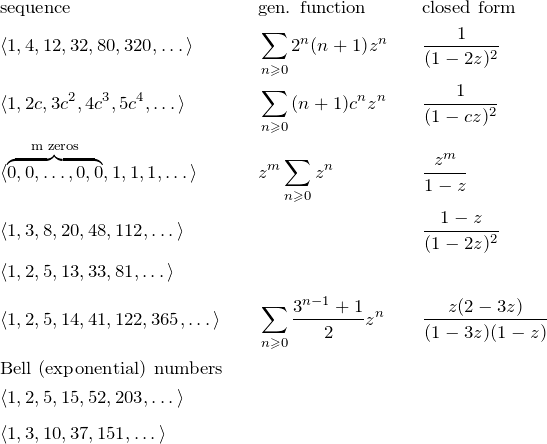
All the ways to write an integer ![]() as a sum of 1s, 2s and 3s. Each representation
as a sum of 1s, 2s and 3s. Each representation ![]() is encoded by a monomial
is encoded by a monomial ![]() that appears in the coefficient polynomial of
that appears in the coefficient polynomial of ![]() :
:
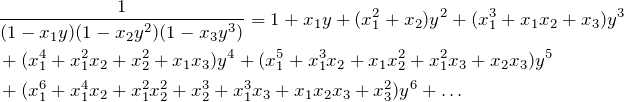
![]()
Some simple sequences and their generating functions
![Rendered by QuickLaTeX.com \begin{align*} &\mathsf{sequence} &&\mathsf{gen.\; function} &&\mathsf{closed\; form}\\ &\seqd{1,0,0,0,0,0} &&\sumzn{[n=0]} &&1\\ &\seqd{0,\dots,0,1,0,0} &&\sumzn{[n=m]} &&z^m \\ &\seqd{1,1,1,1,1,1} &&\sumzn{} && \fr{1-z}\\ &\seqd{1,-1,1,-1,1,-1} &&\sumzn{(-1)^n} && \fr{1+z}\\ &\seqd{1,0,1,0,1,0} &&\sumzn{[2\backslash n]} && \fr{1-z^2}\\\ &\seqd{1,0,\dots,0,1,0,\dots,0,1,0} &&\sumzn{[m\backslash n]} && \fr{1-z^m}\\ &\seqd{1,2,3,4,5,6} &&\sumzn{(n+1)} && \fr{(1-z)^2}\\ &\text{Triangular numbers}&& && \\ &\seqd{1,3,6,10,15,21} &&\sumzn{\binom{n+2}{2}} && \fr{(1-z)^3}\\ &\text{Tetrahedral numbers}&& && \\ &\seqd{1,4,10,20,35} &&\sumzn{\binom{n+3}{3}} && \fr{(1-z)^4}\\ &\seqd{1,5,15,35,70} &&\sumzn{\binom{n+4}{4}} && \fr{(1-z)^5}\\ &\textstyle\seqd{1,c,\binom{c+1}{2}, \binom{c+2}{3}} &&\displaystyle\sumzn{\binom{c+n-1}{n}} && \fr{(1-z)^c}\\ &\text{equivalent to} &&\sumzn{\binom{n+k}{k}} && \fr{(1-z)^{k+1}}\\ \end{align*}](https://www.adamponting.com/wp-content/ql-cache/quicklatex.com-8401ff63180e325c1606874e78e444e3_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} &\seqd{0,1,4,9,16} &&\sumzn{n^2} && \frac{z(z+1)}{(1-z)^3}\\ &\seqd{1,2,4,8,16,32} &&\sumzn{2^n} && \fr{1-2z}\\ &\seqd{1,4,6,4,1,0,0} &&\sumzn{ \binom{4}{n}} && (1+z)^4\\ &\textstyle\seqd{1,c,\binom{c}{2}, \binom{c}{3}} &&\sumzn{\binom{c}{n}} && (1+z)^c\\ &\seqd{1,c,c^2,c^3} &&\sumzn{c^n}&& \fr{1-cz}\\ &\seqd{0,1,\fr{2},\fr{3},\fr{4}} &&\snge[1] \fr{n}z^n && \ln\fr{1-z}\\ &\langle 0,1,-\fr{2},\fr{3},-\fr{4},\dots\rangle &&\snge[1] \frac{-1^{n+1}}{n}z^n && \ln (1+z) \\ &\langle 1,1,\fr{2},\fr{6},\fr{24},\fr{120},\dots\rangle &&\sumzn{\frac{1}{n!}} && e^z\\ &\seqd{0,1,0,\fr{3!},0,\fr{5!}} && \sumzn{\fr{n!}[2\backslash (n+1)]} && \sin{z}\\ &\seqd{1,0,\fr{2!},0,\fr{4!},0} && \sumzn{\fr{n!}[2\backslash (n+2)]} && \cos{z}\\ &\seqd{} && \sumzn{} && \\ \end{align*}](https://www.adamponting.com/wp-content/ql-cache/quicklatex.com-225ed61a2a84eb08c1f2d2b185c69951_l3.png)
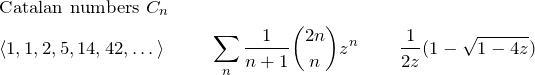
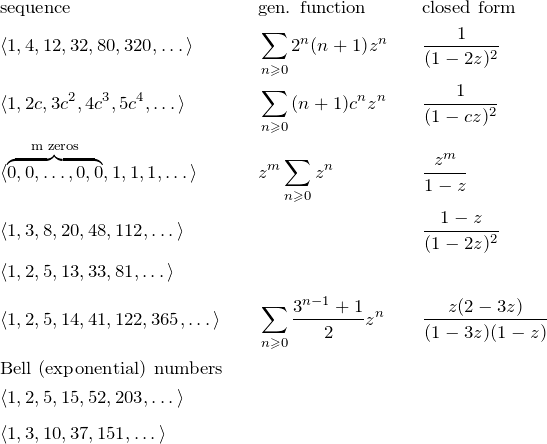
All the ways to write an integer ![]() as a sum of 1s, 2s and 3s. Each representation
as a sum of 1s, 2s and 3s. Each representation ![]() is encoded by a monomial
is encoded by a monomial ![]() that appears in the coefficient polynomial of
that appears in the coefficient polynomial of ![]() :
: