Last year I became fascinated by squared squares and its history and theory – e.g. see this page on the algebraic and network methods of constructing them. I wrote a program to find if there were packings for squares of side 
. Packings? I don’t know what to call them – unlike the business of squaring squares and rectangles, I’m not concerned about the shape of the boundary. The program found packings for 9, 25 and 49 squares, and there’s a simple regular pattern that can be extended to work with any odd 
.
Here’s the 7×7 = 49 square version
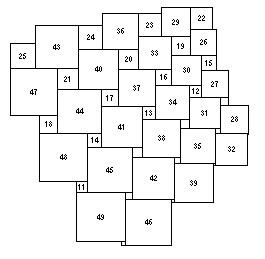
The 9×9 = 81 square version.
The 11×11 = 121 square version.
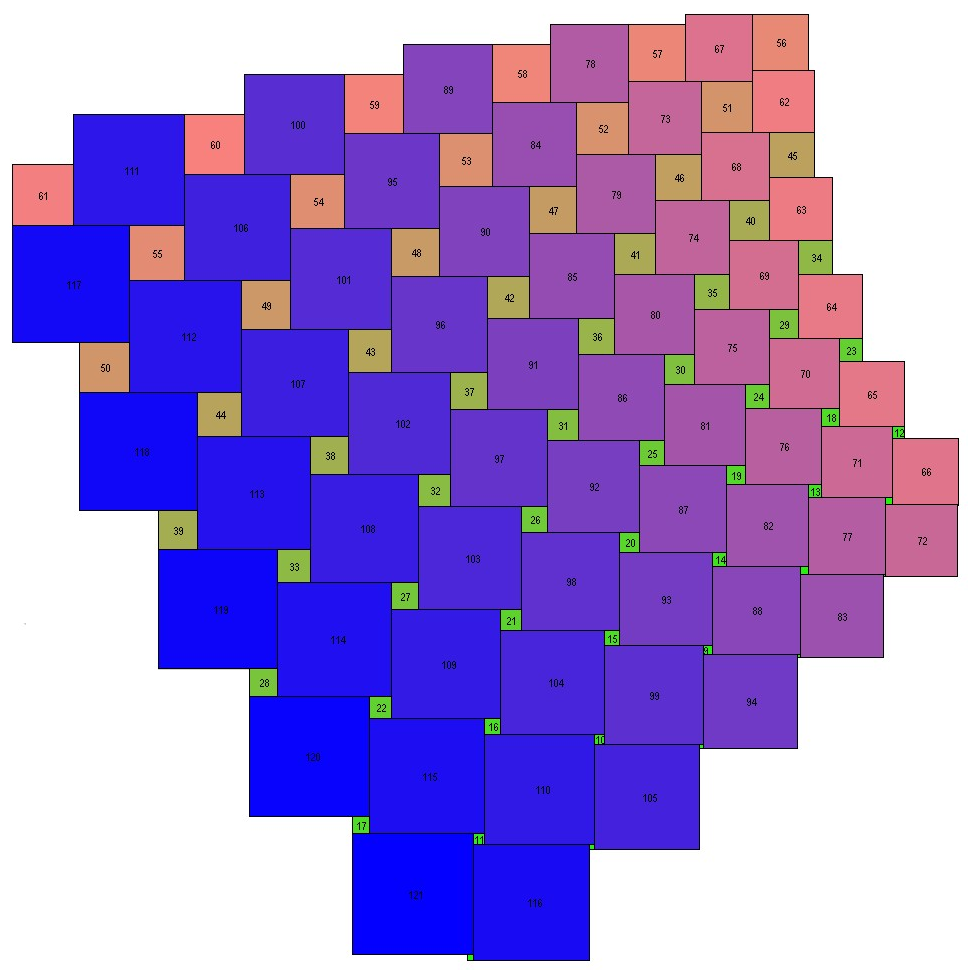
[May 2014]
Hello Adam – Hope you are well. My name is Winnie and I am an origami designer specialising in folding geometric corrugations. I am currently reading through Robert Fathauer’s new book and found your square packing work.
I am wondering if you know whether anyone has done work on non-edge to edge multi-sized triangle (scalene or equilateral), packing? The reason I am wondering, is because I have a method of using non-edge to edge tessellations as a base for some origami work. And the one thing I have struggled with, is to find a way to pack triangles of different sizes (as well as irregular hexagons) into a plane, in a non edge to edge way. I do have a maths degree – but it’s in mostly applied and statistics. So my geometry skills are completely lacking!
(PS I will be turning your square packing into origami – stay tuned 🙂
Cheers
Winnie