An easy method of tiling/squaring the plane with integer squares of sides ![]()
OK, not infinite area, exactly – but a greater area than any specified area, no matter how large – which is what infinite means, in practice, I guess. Seems to work the same for each ![]() .
.
It’s by using an ![]() arrangement of squares, with any odd
arrangement of squares, with any odd ![]() , a similar simple arrangement for each one, e.g. with
, a similar simple arrangement for each one, e.g. with ![]() = 7, 9, 11: (49, 81, 121 squares)
= 7, 9, 11: (49, 81, 121 squares)
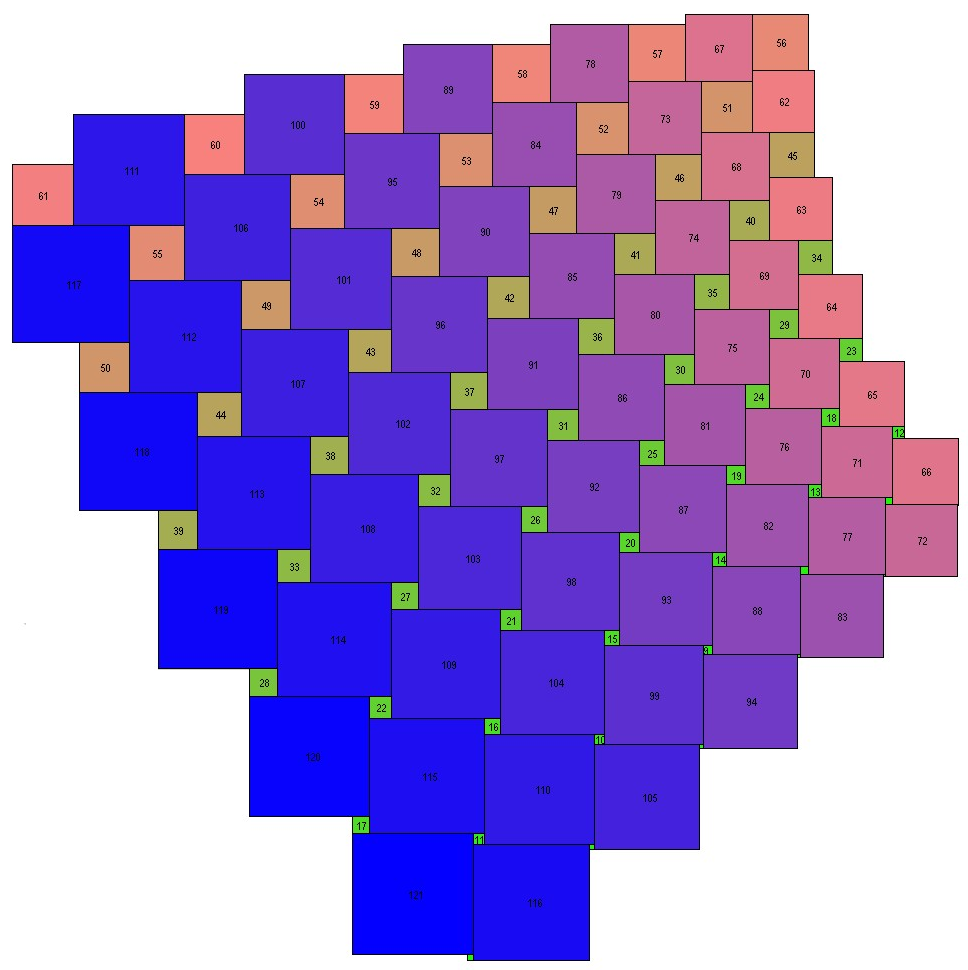
How to number the squares:
1. Begin at bottom right corner of an
2. Start at top right, going down the columns, filling the remaining gaps, and moving R to L. i.e. first the rightmost column. Top square is already filled, put
Maybe easier to see than explain. e.g. for the 5×5 square:
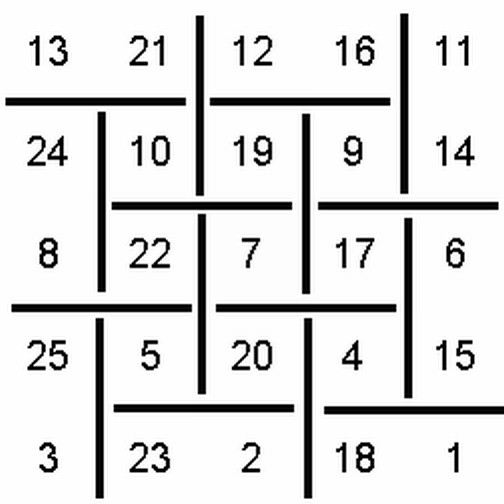
Squares are arranged with what I call alternating h-lines and v-lines, shown as black lines in the picture. An h-line is a horizontal line segment with two squares on each side of it, a v-line, a vertical line segment with two squares on each side. The arrangement has a h-line on the top left, v-line on the top right.

Very beautiful!