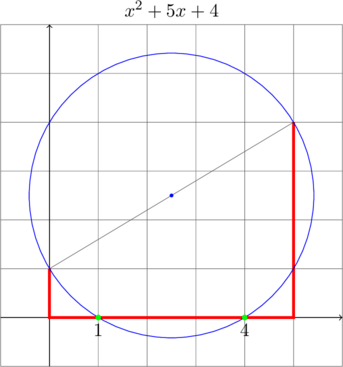
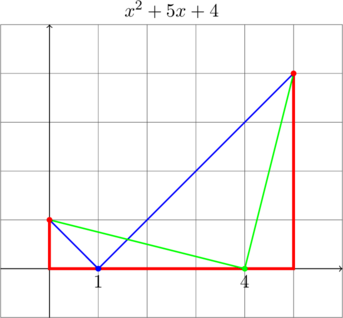
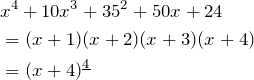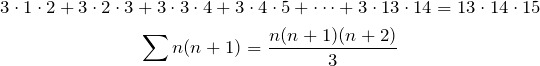genfrac{left-delim}{right-delim}{thickness}{mathstyle}
{numerator}{denominator}

   

   

   

Like this:

   

[a+AB b-A^2]
[c-A^2 d+AB]

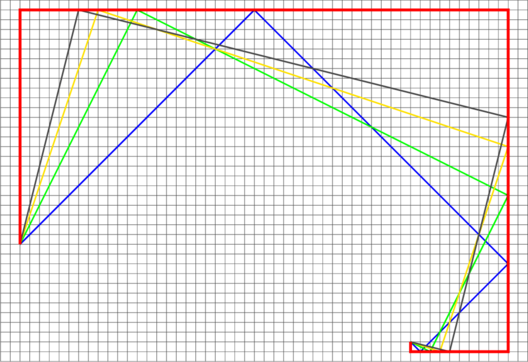
Moving north-east A times produces:

.
Moving north-east A times produces: .
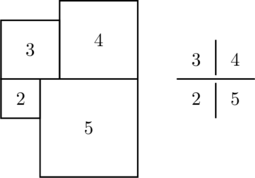
How to construct:
Start with any h-line: four squares along a horizontal line with , e.g. :

Extend the arithmetic progressions along the diagonals:

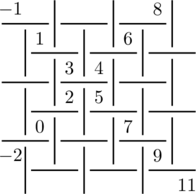
Then fill in a diagonal next to one of these 2, with any arithmetic progression. e.g:

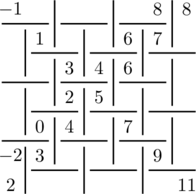
Then all the empty squares have been determined and can be filled in, making the sums equal across all line segments (the h-lines and v-lines).
Then when drawing the squaring, draw the squares of negative size on the other side of the line from where they ‘should’ be, e.g. :

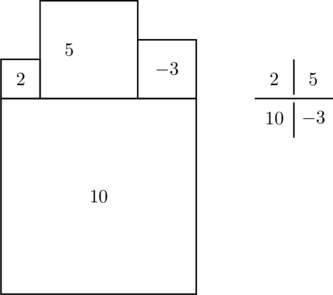
It seems that any grid of numbers constructed this way makes a tesselation of the plane.

Also, it seems that all the -sized squares (I mark them with a small circle on the squaring) lie in a straight line, no matter what sequences are used. I’m sure there’s an obvious reason for that!

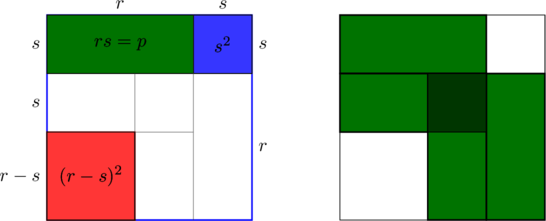
Unfortunately TikZ has too many bugs with barycentric plotting. ARGGHH! Unusable. Not slight – massive and weird errors.

   

Nonregular CFs can also be represented as squares in a rectangle.

   

   

---

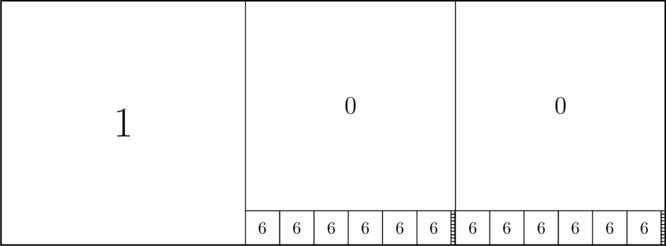
e.g.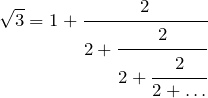

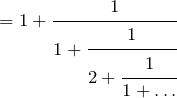
Picture of : 1/(1+1/(1+1/(1+etc

   

---

---