When the curve meets a lattice point ![]() in this picture, it means that there
in this picture, it means that there ![]() has an integer value. I put the prime
has an integer value. I put the prime ![]() in red. Notice that the red line marked
in red. Notice that the red line marked ![]() has no dots, while the
has no dots, while the ![]() line has. This pattern is the same for all primes one less and one more than a multiple of 4.
line has. This pattern is the same for all primes one less and one more than a multiple of 4.
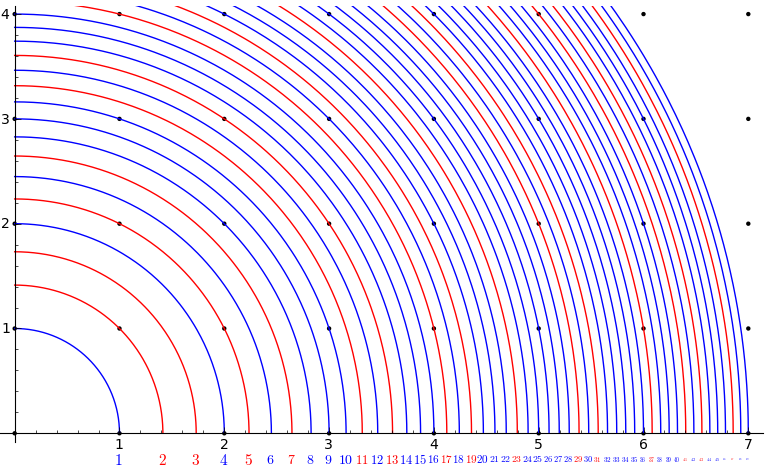
The primes ![]() : (all crossing lattice points)
: (all crossing lattice points)
The primes ![]() : (none cross lattice points)
: (none cross lattice points)
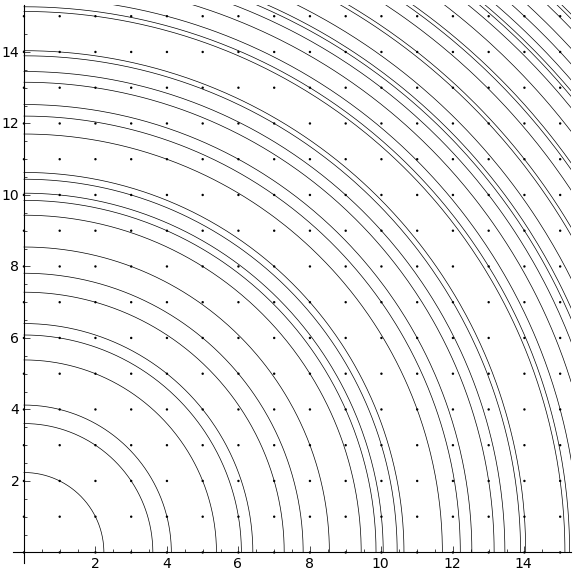
In these next pics, all possible values of ![]() are shown,
are shown, ![]() and
and ![]() integers
integers ![]() , up to a certain
, up to a certain ![]() .
.
Why there should be vertical gaps is explained by modular arithmetic and residues.
“Of two numbers possessing no common divisor one is called the quadratic residue of the other when it is congruent to a square number with respect to the other as modulus; if there is no such square number it is called a quadratic nonresidue. For example, ![]() is a quadratic residue of
is a quadratic residue of ![]() , since
, since ![]() ;
; ![]() is a quadratic nonresidue of
is a quadratic nonresidue of ![]() , since there exists no square number
, since there exists no square number ![]() such that
such that ![]() .” (Dörrie)
.” (Dörrie)
I don’t know if there’s a name for the equivalent thing with sums of squares; for now I’ll call it the biquadratic residue.
Since ![]() is always
is always ![]() or
or ![]() ,
, +++ ![]() . (i.e.
. (i.e. ![]() is a biquadratic nonresidue of
is a biquadratic nonresidue of ![]() .)
.)
Since ![]() is
is ![]() ,
, ![]() or
or ![]() ,
, +++ ![]() .
.
Since ![]() is
is ![]() ,
, ![]() ,
, ![]() or
or ![]() ,
, +++ ![]() .
.
![]() numbers to a row, i.e. the top line of the image shows, for the numbers
numbers to a row, i.e. the top line of the image shows, for the numbers ![]() to
to ![]() , a black dot where there are values of
, a black dot where there are values of ![]() and
and ![]() such that
such that ![]() . Up to
. Up to ![]() . (700 rows)
. (700 rows)
In these next pics, only the top-leftmost part is shown.
Rows of ![]() (i.e. only about the leftmost
(i.e. only about the leftmost ![]() th of the row shown)
th of the row shown)
Detail of the upper-left corner of previous picture. The top row pixels are black if there are values of ![]() and
and ![]() such that
such that ![]() ; the 2nd row represents
; the 2nd row represents ![]() etc.
etc.

In the following picture, the pixels of the ![]() th row show whether
th row show whether ![]() up to
up to ![]() are biquadratic residues of
are biquadratic residues of ![]() or not. i.e. the white pixels show the “gaps” (biquadratic nonresidues) where no
or not. i.e. the white pixels show the “gaps” (biquadratic nonresidues) where no ![]() (mod
(mod ![]() ) can ever land.
) can ever land.
All the preceding pictures use one modulus (row length) for the entire image; in these ones, each row is a different modulus.
Gaps, approx. ![]() up to
up to ![]()

Gaps, approx. ![]() to
to ![]() .
.
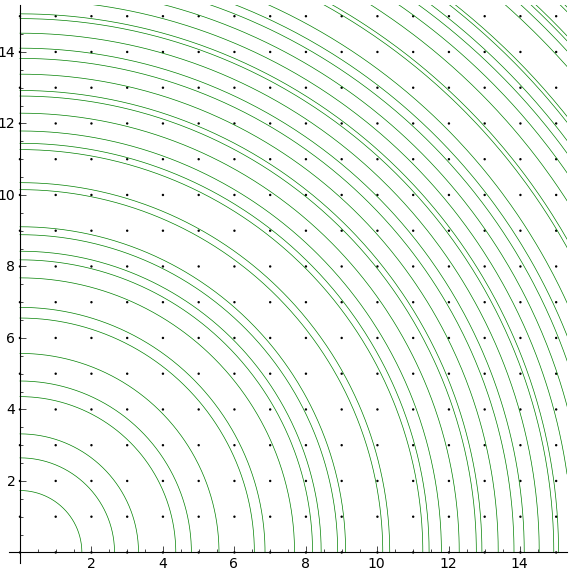
Gaps, approx. ![]() –
–![]() .
.
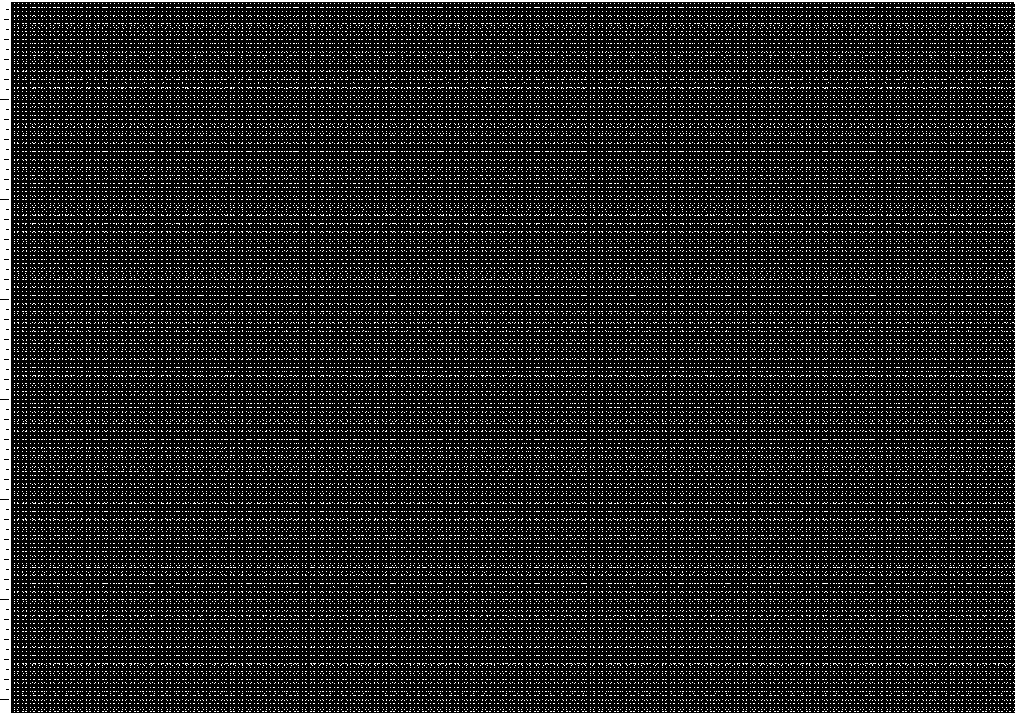
Gaps, approx. ![]() –
–![]()
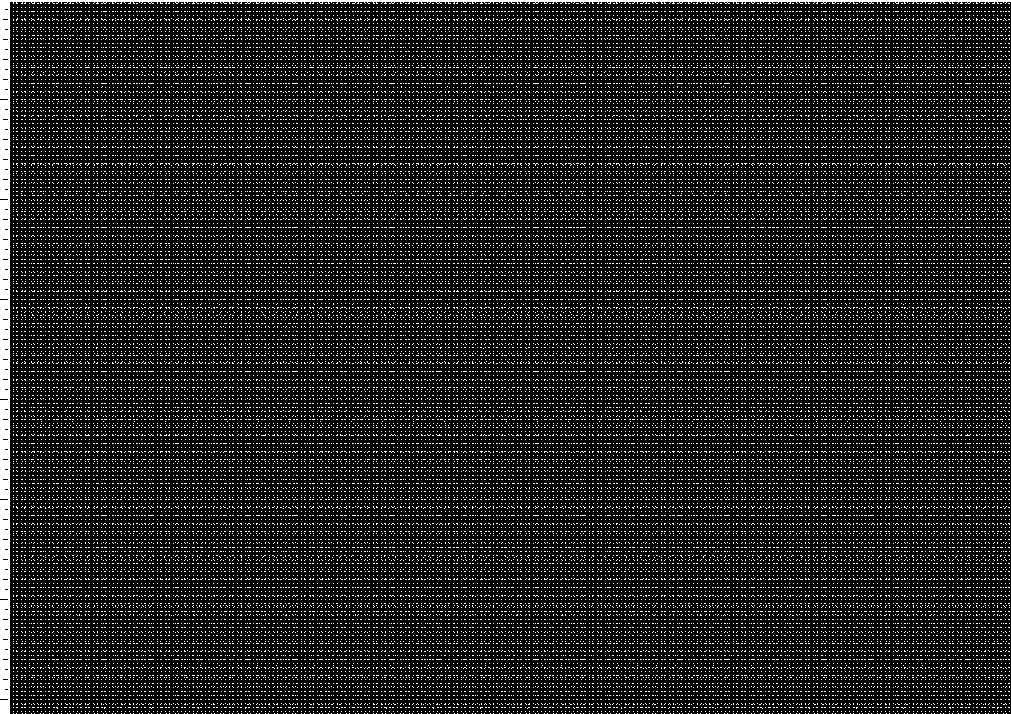
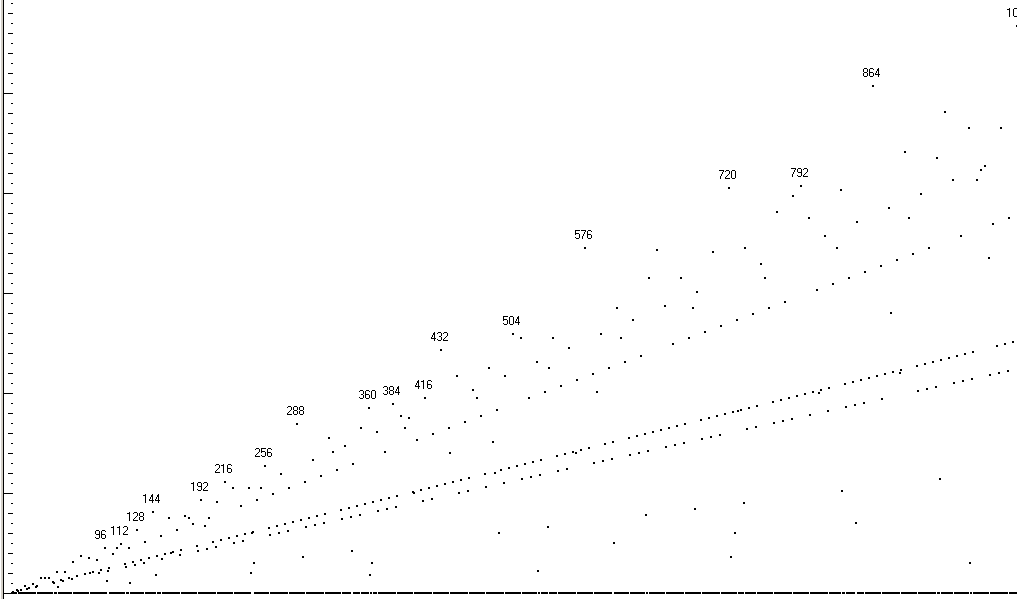
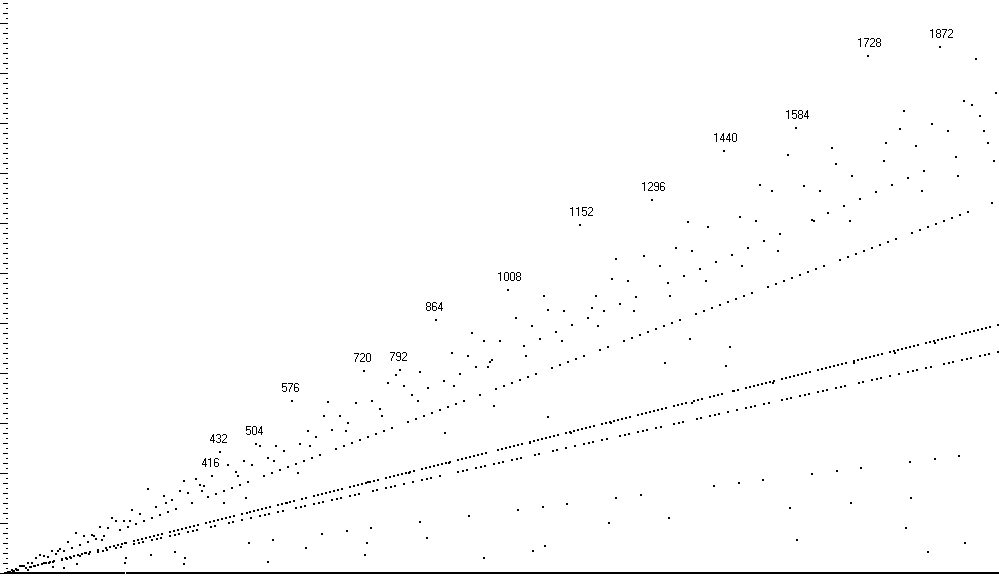
The next pictures summarize the last ones, and plot the number of (biquadratic nonresidue) gaps (y-axis) for each modulus (x-axis). The labelled points are those moduli that have a larger number of gaps than any smaller modulus.
Number of gaps, moduli ![]() –
–![]()
Number of gaps, moduli ![]() –
–![]()
Some more ![]() pictures, with rows the length of some of those “record” moduli.
pictures, with rows the length of some of those “record” moduli.
Rows of ![]() =
= ![]()

Rows of ![]() =
= ![]() . (the right edge past
. (the right edge past ![]() is cut off)
is cut off)

Rows of ![]() =
= ![]() . (Left 2/3 of the rows shown)
. (Left 2/3 of the rows shown)

List of gaps, to ![]()
Gaps mod 4=2.2 : 3 (i.e. there are no integer values of ![]() and
and ![]() such that
such that ![]() .)
.)
Gaps mod 8=2.2.2 : 3, 6, 7
Gaps mod 9=3.3 : 3, 6
Gaps mod 12=2.2.3 : 3, 7, 11
Gaps mod 16=2.2.2.2 : 3, 6, 7, 11, 12, 14, 15
Gaps mod 18=2.3.3 : 3, 6, 12, 15
Gaps mod 20=2.2.5 : 3, 7, 11, 15, 19
Gaps mod 24=2.2.2.3 : 3, 6, 7, 11, 14, 15, 19, 22, 23
Gaps mod 27=3.3.3 : 3, 6, 12, 15, 21, 24
Gaps mod 28=2.2.7 : 3, 7, 11, 15, 19, 23, 27
Gaps mod 32=2.2.2.2.2 : 3, 6, 7, 11, 12, 14, 15, 19, 22, 23, 24, 27, 28, 30, 31
Gaps mod 36=2.2.3.3 : 3, 6, 7, 11, 12, 15, 19, 21, 23, 24, 27, 30, 31, 33, 35
Gaps mod 40=2.2.2.5 : 3, 6, 7, 11, 14, 15, 19, 22, 23, 27, 30, 31, 35, 38, 39
Gaps mod 44=2.2.11 : 3, 7, 11, 15, 19, 23, 27, 31, 35, 39, 43
Gaps mod 45=3.3.5 : 3, 6, 12, 15, 21, 24, 30, 33, 39, 42
Gaps mod 48=2.2.2.2.3 : 3, 6, 7, 11, 12, 14, 15, 19, 22, 23, 27, 28, 30, 31, 35, 38, 39, 43, 44, 46, 47
Gaps mod 49=7.7 : 7, 14, 21, 28, 35, 42
Gaps mod 52=2.2.13 : 3, 7, 11, 15, 19, 23, 27, 31, 35, 39, 43, 47, 51
Gaps mod 54=2.3.3.3 : 3, 6, 12, 15, 21, 24, 30, 33, 39, 42, 48, 51
Gaps mod 56=2.2.2.7 : 3, 6, 7, 11, 14, 15, 19, 22, 23, 27, 30, 31, 35, 38, 39, 43, 46, 47, 51, 54, 55
Gaps mod 60=2.2.3.5 : 3, 7, 11, 15, 19, 23, 27, 31, 35, 39, 43, 47, 51, 55, 59
Gaps mod 63=3.3.7 : 3, 6, 12, 15, 21, 24, 30, 33, 39, 42, 48, 51, 57, 60
Gaps mod 64=2.2.2.2.2.2 : 3, 6, 7, 11, 12, 14, 15, 19, 22, 23, 24, 27, 28, 30, 31, 35, 38, 39, 43, 44, 46, 47, 48, 51, 54, 55, 56, 59, 60, 62, 63
Gaps mod 68=2.2.17 : 3, 7, 11, 15, 19, 23, 27, 31, 35, 39, 43, 47, 51, 55, 59, 63, 67
Gaps mod 72=2.2.2.3.3 : 3, 6, 7, 11, 12, 14, 15, 19, 21, 22, 23, 24, 27, 30, 31, 33, 35, 38, 39, 42, 43, 46, 47, 48, 51, 54, 55, 57, 59, 60, 62, 63, 66, 67, 69, 70, 71
Gaps mod 76=2.2.19 : 3, 7, 11, 15, 19, 23, 27, 31, 35, 39, 43, 47, 51, 55, 59, 63, 67, 71, 75
Gaps mod 80=2.2.2.2.5 : 3, 6, 7, 11, 12, 14, 15, 19, 22, 23, 27, 28, 30, 31, 35, 38, 39, 43, 44, 46, 47, 51, 54, 55, 59, 60, 62, 63, 67, 70, 71, 75, 76, 78, 79
Gaps mod 81=3.3.3.3 : 3, 6, 12, 15, 21, 24, 27, 30, 33, 39, 42, 48, 51, 54, 57, 60, 66, 69, 75, 78
Gaps mod 84=2.2.3.7 : 3, 7, 11, 15, 19, 23, 27, 31, 35, 39, 43, 47, 51, 55, 59, 63, 67, 71, 75, 79, 83
Gaps mod 88=2.2.2.11 : 3, 6, 7, 11, 14, 15, 19, 22, 23, 27, 30, 31, 35, 38, 39, 43, 46, 47, 51, 54, 55, 59, 62, 63, 67, 70, 71, 75, 78, 79, 83, 86, 87
Gaps mod 90=2.3.3.5 : 3, 6, 12, 15, 21, 24, 30, 33, 39, 42, 48, 51, 57, 60, 66, 69, 75, 78, 84, 87
Gaps mod 92=2.2.23 : 3, 7, 11, 15, 19, 23, 27, 31, 35, 39, 43, 47, 51, 55, 59, 63, 67, 71, 75, 79, 83, 87, 91
Gaps mod 96=2.2.2.2.2.3 : 3, 6, 7, 11, 12, 14, 15, 19, 22, 23, 24, 27, 28, 30, 31, 35, 38, 39, 43, 44, 46, 47, 51, 54, 55, 56, 59, 60, 62, 63, 67, 70, 71, 75, 76, 78, 79, 83, 86, 87, 88, 91, 92, 94, 95
Gaps mod 98=2.7.7 : 7, 14, 21, 28, 35, 42, 56, 63, 70, 77, 84, 91
Gaps mod 99=3.3.11 : 3, 6, 12, 15, 21, 24, 30, 33, 39, 42, 48, 51, 57, 60, 66, 69, 75, 78, 84, 87, 93, 96
Gaps mod 100=2.2.5.5 : 3, 7, 11, 15, 19, 23, 27, 31, 35, 39, 43, 47, 51, 55, 59, 63, 67, 71, 75, 79, 83, 87, 91, 95, 99
“Record” gaps.
4 (2.2) has 1 gap. (i.e. ![]() : there are no integer values of
: there are no integer values of ![]() and
and ![]() such that
such that ![]() .)
.)
8 (2.2.2) has 3 gaps.
16 (2.2.2.2) has 7 gaps.
24 (2.2.2.3) has 9 gaps.
32 (2.2.2.2.2) has 15 gaps.
48 (2.2.2.2.3) has 21 gaps.
64 (2.2.2.2.2.2) has 31 gaps.
72 (2.2.2.3.3) has 37 gaps.
96 (2.2.2.2.2.3) has 45 gaps.
112 (2.2.2.2.7) has 49 gaps.
128 (2.2.2.2.2.2.2) has 63 gaps.
144 (2.2.2.2.3.3) has 81 gaps.
192 (2.2.2.2.2.2.3) has 93 gaps.
216 (2.2.2.3.3.3) has 111 gaps.
256 (2.2.2.2.2.2.2.2) has 127 gaps.
288 (2.2.2.2.2.3.3) has 169 gaps.
360 (2.2.2.3.3.5) has 185 gaps.
384 (2.2.2.2.2.2.2.3) has 189 gaps.
416 (2.2.2.2.2.13) has 195 gaps.
432 (2.2.2.2.3.3.3) has 243 gaps.
504 (2.2.2.3.3.7) has 259 gaps.
576 (2.2.2.2.2.2.3.3) has 345 gaps.
720 (2.2.2.2.3.3.5) has 405 gaps.
792 (2.2.2.3.3.11) has 407 gaps.
864 (2.2.2.2.2.3.3.3) has 507 gaps.
1008 (2.2.2.2.3.3.7) has 567 gaps.
1152 (2.2.2.2.2.2.2.3.3) has 697 gaps.
![]()
1872 (2.2.2.2.3.3.13) has 1053 gaps.
2016 (2.2.2.2.2.3.3.7) has 1183 gaps.
2160 (2.2.2.2.3.3.3.5) has 1215 gaps.





