Euler 1755.
(aka Euler’s method, Euler transform, Euler summation)
Derivation
Buchanan & Turner give a very simple derivation using difference operators and their basic properties.
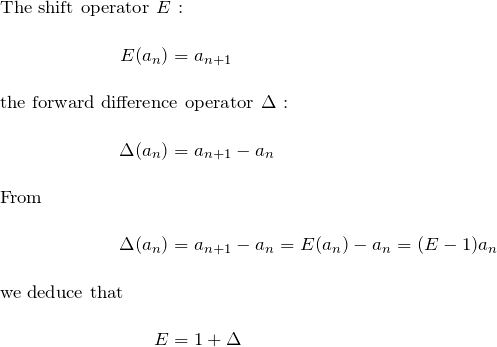
Consider the summation of an alternating series:
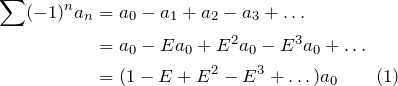
![]()
Since ![]() is the RHS of
is the RHS of ![]() , with
, with ![]() , we have:
, we have:
![]()
Substituting in ![]() :
:
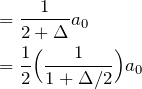
Substituting in ![]() with
with ![]() gets the Euler transform:
gets the Euler transform:
![Rendered by QuickLaTeX.com \[\sum\limits_{n=0}^\infty (-1)^n a_n&=\frac{1}{2}(1-\frac{\Delta}{2}+\frac{\Delta^2}{4}-\frac{\Delta^3}{8}+\frac{\Delta^4}{16}-\dots)a_0\]](https://www.adamponting.com/wp-content/ql-cache/quicklatex.com-487c04717ab8ea2c83e8fe3d1f4a1a47_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\sum\limits_{n=0}^\infty (-1)^n a_n=\fr{2}\sum\limits_{i=0}^\infty \frac{(-1)^i}{2^i}\Delta^i a_0}\quad \text{(3)}\]](https://www.adamponting.com/wp-content/ql-cache/quicklatex.com-0bac47c114a1eaa1641efe64ed7b9020_l3.png)
Hamming in Numerical Methods gives a more complicated derivation using summation by parts, arriving at the more general form:
![Rendered by QuickLaTeX.com \[\sum\limits_{k=0}^\infty a_k t^k = \fr{1-t}\sum\limits_{i=0}^\infty \big( \frac{t}{1-t}\big)^i \Delta^i a_0 \]](https://www.adamponting.com/wp-content/ql-cache/quicklatex.com-5a51795c28d65054eab70106eb94da96_l3.png)
He says “the most frequent case of application is when ![]() ” (i.e. the form in equation
” (i.e. the form in equation ![]() ) and gives as an example of its use to make a series converge faster:
) and gives as an example of its use to make a series converge faster:
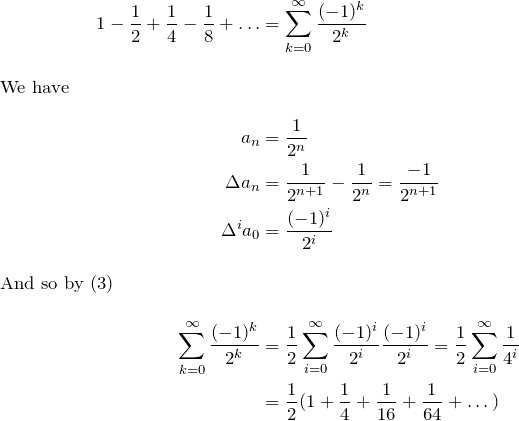
which converges more quickly.
(but e.g. with the series ![]() , in Hamming’s formula
, in Hamming’s formula ![]() is
is ![]() , and the transformation converges no more quickly.)
, and the transformation converges no more quickly.)
Numerical Recipes says “Generally it is advisable to do a small number of terms directly, through term ![]() , and then apply the transformation to the rest of the series beginning with term
, and then apply the transformation to the rest of the series beginning with term ![]() . The formula (for
. The formula (for ![]() even) is
even) is
![Rendered by QuickLaTeX.com \[\sum\limits_{s=0}^\infty (-1)^s a_s = a_0-a_1+a_2\dots-a_{n-1}+\sum\limits_{s=0}^\infty \frac{(-1)^s}{2^{s+1}}[\Delta^s a_n] \]](https://www.adamponting.com/wp-content/ql-cache/quicklatex.com-9b314e55d989c50696e46f2586d9d277_l3.png)
the Euler transform is “the result of applying the binomial transform to the sequence associated with [a sequence’s] ordinary generating function.” – wikip, ‘binomial transform’
references
Buchanan, Turner – Numerical Methods and Analysis
Richard Hamming – Numerical methods for scientists and engineers
Numerical Recipes, 3rd ed., Ch.5