Fermat’s little theorem

If $p$ is prime, and $p \nmid a$ , (i.e. $\gcd(a,p)=1$ ) then

(1) $\begin{equation*} \boxed{a^{p-1}\equiv 1\pmod p} \end{equation*}$

Or equivalently, if $p$ is prime, then

(2) $\begin{equation*} \boxed{a^{p}\equiv a\pmod p} \end{equation*}$

Stated by Fermat 1640. Proved by Euler 1736, and by Leibniz (unpublished) about 50 years before that.

Proof
$\gcd(a,p)=1$ means that $a$ has an inverse $\pmod p$ , i.e. there’s a number $n$ such that $na\equiv 1 \pmod p$ .
The numbers $1,2,\dots,p-1$ also have inverses $\pmod p$ , because $p$ is prime.
Consider the remainders of $a,2a,\dots,(p-1)a$ on division by $p$ :

$a \pmod p, \quad 2a \pmod p, \quad \dots, \quad (p-1)a \pmod p.$

These are the numbers $1,2,\dots p-1$ again in a different order, as they are nonzero and unequal $\pmod p$ , since $ja \equiv ka \pmod p$ would imply $j \equiv k \mod p$ . It follows that:

$\begin{gather*} a\times 2a \times \cdots \times (p-1)a\equiv 1\times 2\times \cdots \times (p-1) \pmod p, \intertext{i.e.} a^{p-1}\times a \times \cdots \times (p-1)\equiv 1\times 2\times \cdots \times (p-1) \pmod p, \intertext{and therefore} a^{p-1}\equiv 1\pmod p \end{gather*}$

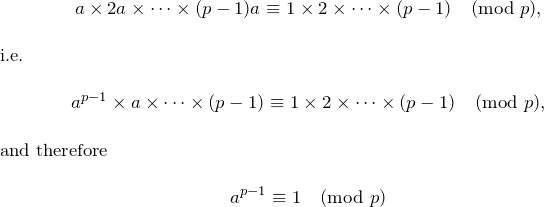
Proof by induction (for $a>0$ )
1. When $a=1$ , obviously $1^p\equiv 1\pmod p$ .
2. Assuming $a^{p}\equiv a\pmod p$ is true for every prime $p$ , prove $(a+1)^{p}\equiv a+1\pmod p$ .
From the binomial theorem,