Fractions constructible with n different-sized squares

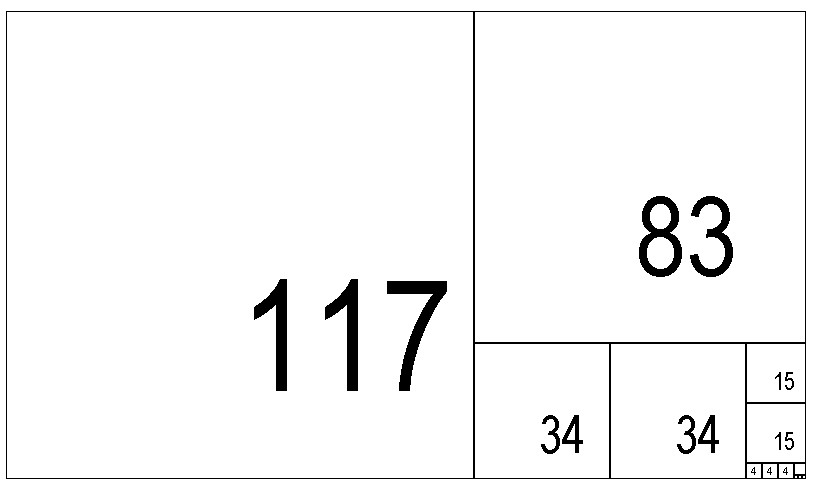
A ratio, e.g. 200/117, is represented as a 200×117 rectangle. Operation of the Euclidean algorithm or the jigsaw method gives the continued fraction [1;1,2,2,3,1,3].

On this page, variables are positive integers. Rectangles $x\times y$ are drawn only for $x\geq y$ , but usually in the text, only the proper fractions with $x<y$ are given, to save space (and these lie conveniently between 0 and 1.) But remember, the rectangle $x\times y$ represents both $x/y$ and $y/x$ e.g. where $3/4$ appears below, $4/3$ also has the same number and size of constituent squares, it is just rotated $90^{\circ}$ (which here = inversion).

1 size

1 square alone is $n/n$ or $1$ .
Putting 2, 3, 4… squares next to each other, we have the numbers 2, 3, 4.. or, looking from the $y$ direction, $1/2$ , $1/3$ , $1/4$ …
i.e. numbers of the form $n$ and $1/n$
In order of magnitude: $1,2,3,4,\dots$
Or, from the $y$ direction, $\dots 1/4,1/3,1/2$

N.B. From here on I will omit all mention of the half of the fractions $>1$ , except in the general formulas, to save space. For every $x/y$ mentioned, $y/x$ is in the same group.

2 sizes

Using 1 large square and smaller ones along the side, we get $2/3, 3/4, 4/5 \dots$
[illustrate]
Using 2 squares and smaller ones along the side, $2/5, 3/7, 4/9 \dots$
[illustrate a few]
Using 3 and smaller ones, $2/7, 3/10, 4/13\dots$
[show a few]
i.e. numbers of the form $\displaystyle \frac{n}{an+1}$ (and $\displaystyle \frac{an+1}{n}$ ), where $n\geq 2$ .
[show diagram of general case]
In order of magnitude:
$\dots 2/9,3/13,4/17,5/21\dots \frac{n}{4n+1},2/7,3/10,4/13,5/16,\dots \frac{n}{3n+1},$
$2/5,3/7,4/9,5/11\dots\frac{n}{2n+1},2/3, 3/4, 4/5, 5/6 \dots \frac{n}{n+1}$

[picture of plot of these on number line, $0<a/b<l$ , each a short vertical line, maybe pic width 500px]

3 sizes
Working backwards, this group is made up of each of the previous group, with 1 or more squares stuck on to the side.
From the “2 sizes, 1 large square group”:
$2/3$ with 3×3 squares added makes: $3/5,3/8,3/11,3/14\dots$
$3/4$ with 4×4 squares added makes: $4/7,4/11,4/15,4/19\dots$
$4/5$ with 5×5 squares added makes: $5/9,5/14,5/19,5/24\dots$ etc.

4 sizes

Functions

Define:
$\Delta(a/b)=$ the number of Different-sized squares needed to construct $a/b$ .
$=$ number of iterations of Euclid’s algorithm to find $gcd(a,b)$
$=$ number of terms $[a_0;a_1,a_2,a_3\dots]$ in the continued fraction.

$N(a/b)=$ the total Number of squares needed to construct $a/b$ , regardless of size.
$=$ sum of the continued fraction terms $[a_0;a_1,a_2,a_3\dots]$ .
$=$ total of the numbers $n$ used as multipliers $a=nb+c$ in Euclid’s algorithm.

If a/b is irrational, $N(a/b)$ is infinite, e.g. $N(\pi/1)=\infty$ . Although e.g. for $[1;2,1,1,2,1,1,1,2\dots]$ = VALUE*#*#*#?!?, $N()=\infty$ but $\Delta()=2$ .

[picture of Stern-Brocot tree, $0<a/b<1$ , with D() and N() next to each number. width =500px?]

=== state rules for D and N for S-B tree. and for adding fractions generally.

=== make table of D and table of N for a=1…50 and b=1…50 .. or 30, whatever fits on a page.
===could do a table 100×100 with dots in each square representing D(a/b).. or colour coded.. could go higher.
=== what WOULD that look like?! 🙂 or even 500×500, 2 pixel colour in each one… 250×250 maybe better.

=== How many fractions have $N()$ =1,2,3..? is is Catalan numbers or something?

=== Make another page for the 3D case!!

adamponting.com

Fractions constructible with n different-sized squares

Leave a Reply Cancel reply