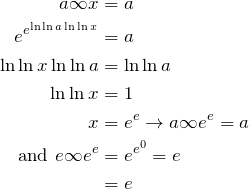I was wondering (not for the first time) what comes next in the progression ![]() ,
, ![]() ,
, ![]() …
… ![]()
Probably this is a thing already. Anyway…
What is ![]() ?
?
Well, my idea was that ![]() , so
, so ![]()
So then ![]() . Sounds reasonable. (and silly.)
. Sounds reasonable. (and silly.)
Hmm so what’s the “I”, like ![]() and
and ![]() ?
?
![]()
Hmm interesting hehe.
And ![]() ?
?
![]()
Hmm so ![]() .. that’s weird.
.. that’s weird.
Turns out that ![]() is, for
is, for ![]() , very close to
, very close to ![]() .
.
(And obviously for ![]() , very close to
, very close to ![]() .)
.)
It seems once ![]() ,
, ![]() is extremely close to
is extremely close to ![]() .
.
So it’s almost a max function! (just equals the higher value) How strange.
Except if ![]() then
then ![]() .
.
And ![]() is
is ![]()
e.g. ![]() is
is ![]()
![]()
Well, I guess ![]() , so it’s only right that
, so it’s only right that ![]() be
be ![]() .
.
And going the other way, ![]() – why is
– why is ![]() not symmetrical in
not symmetrical in ![]() and
and ![]() like
like ![]() and
and ![]() ? That doesn’t seem right.
? That doesn’t seem right.
So (you guessed it).. maybe call this ![]() .
.

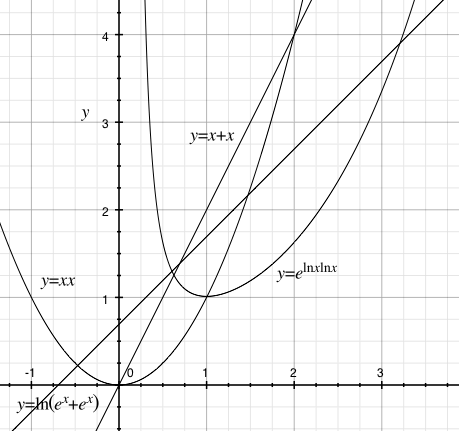
And the next one up? (and down?!)
Call the next one up ![]() maybe..
maybe.. ![]()
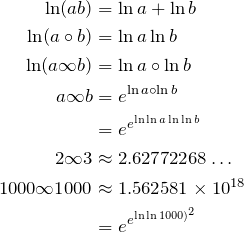
So, find I.