root sequence

$x^p=a$ has a unique root $x>0$ .
There exists an $x_1>0$ such that $x_1^p>a$ .
Define a sequence $x_n>0$ by

$x_{n+1}=\frac{(p-1)x_n+a/x_n^{p-1}}{p}$

$y=\frac{(p-1)x^p+a}{px^{p-1}}$

When $p=2$ ,

$2x_{n+1}=x_n+a/x_n$

With $a=2$ and $x_1=3/2$ , $x^2=17/12$ , and $x^3=(17/12+24/17)/2$ . “This value was once found on a Babylonian tablet of the 18th C BC.”

Graph of $y=\frac{x+2/x}{2}$ , the average of $y=x$ and $y=2/x$ :
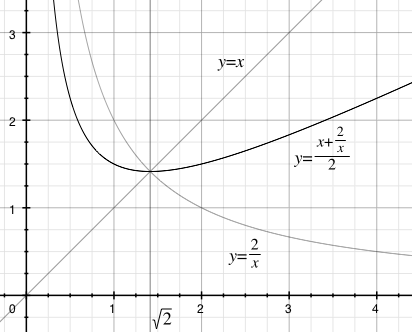
root 2 seq

references

Roger Godement – Analysis I, p108-9

adamponting.com