tests for series convergence/divergence

An infinite series converges if there is a target value $T$ so that for any $L<T$ and any $M>T$ , all the partial sums from some point on lie between $L$ and $M$ .

Cauchy’s approach

This avoids the unreliable rearranging of terms of possibly divergent series, and works instead with finite sums. e.g. in dealing with $\dfrac{1}{1-x}=1+x+x^2+x^3\dots\quad$ :

$\begin{align*} 1&=1-x+x-x^2+x^2-\dots-x^n+x^n \\ &=(1-x)+x(1-x)+x^2(1-x)+\dots+x^{n-1}(1-x)+x^n \\ \fr{1-x}&=1+x+x^2+\dots+x^{n-1}+\frac{x^n}{1-x} \\ &\text{ }1+x+x^2+\dots+x^{n-1}=\fr{1-x}-\frac{x^n}{1-x} \end{align*}$

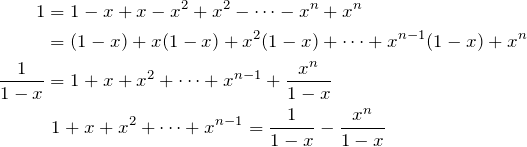
The finite series differs from the target series $T=\dfrac{1}{1-x}$ by

$\frac{x^n}{1-x}$

If we take a value larger than $T$ , is this finite sum eventually below it? If we take a value smaller than $T$ , is this finite sum eventually above it? The value of this series is $\dfrac{1}{1-x}$ if and only if we can make the difference as close to $0$ as we wish by putting a lower bound on $n$ . This happens precisely when $|x| < 1$ . Cauchy’s analysis shows that the equation needs to carry a restriction:

$\fr{1-x}=1+x+x^2+x^3\dots \qquad \text{ when }|x|<1.$

Test for Divergence

If $\lim\limits_{n\to\infty} a_n$ does not exist or if $\lim\limits_{n\to\infty} a_n\neq 0$ , then the series $\sum\limits_{n=1}^\infty a_n$ is divergent.

The Integral Test

If $f$ is a continuous, positive, decreasing function on $[1,\infty)$ , and $a_n=f(n)$ , then the series $\sum\limits_{n=1}^\infty a_n$ is convergent if and only if the improper integral $\int_1^\infty f(x) \;\text{d}x$ is convergent.

The Comparison Test

Suppose $\sum a_n$ and $\sum b_n$ are series with positive terms.
(i) If $\sum b_n$ is convergent and $a_n \les b_n$ for all $n$ , then $\sum a_n$ is also convergent.
(i) If $\sum b_n$ is divergent and $a_n \ges b_n$ for all $n$ , then $\sum a_n$ is also divergent.

Mostly the series $\sum a_n$ is compared with a $p$ -series or a geometric series.

The Limit Comparison Test
Suppose $\sum a_n$ and $\sum b_n$ are series with positive terms. If

$\lim\limits_{n\to\infty} \frac{a_n}{b_n}=c$

where $c$ is a finite number and $c>0$ , then either both series converge or both diverge.

Alternating Series Test

If the alternating series

$\sum\limits_{n=1}^\infty (-1)^{n-1} b_n=b_1-b_2+b_3-b_4+b_5-b_6+\dots \qquad b_n>0$

satisfies ~~+++~~ (i) $b_{n+1} \les b_n\qquad$ for all $n$
~~++++++++++~~ (ii) $\lim\limits_{n\to\infty} b_n=0$
then the series is convergent.

The Ratio Test

The Root Test

Strategy for testing series

references

David Bressoud – A Radical Approach to Real Analysis
James Stewart – Calculus: Early Transcendentals, ch.11

adamponting.com

tests for series convergence/divergence

Leave a Reply Cancel reply