First known appearance in a work of Ibn al-Haytham (965-1039). Stated by Leibniz in an unpublished paper around 1670. Conjectured by John Wilson before 1770. First proved by Lagrange in 1771.
![]()
i.e. if ![]() is prime,
is prime, ![]() divides into
divides into ![]()
Proof: The factors 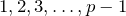 of
of 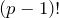 all have inverses
all have inverses 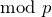 , so each is cancelled by its own inverse except the factors that are inverse to themselves. These are
, so each is cancelled by its own inverse except the factors that are inverse to themselves. These are 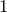 and
and 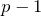 , and no others – because if
, and no others – because if 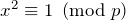 then:
then:
![]()
i.e. ![]() divides
divides ![]() . But then
. But then ![]() divides
divides ![]() or
or ![]() , by the prime divisor property, so
, by the prime divisor property, so
![]()
Thus ![]() ◼
◼
In 1957, F.G. Elston generalized Wilson’s theorem:
Let ![]() be prime and
be prime and ![]() .
.
Then ![]()