Sum of integers
![Rendered by QuickLaTeX.com \[\boxed{1+2+3+4+\dots+n=\frac{n(n+1)}{2}}\]](https://www.adamponting.com/wp-content/ql-cache/quicklatex.com-d0b39ee9658c8ec76dfd0a4db0b2cccc_l3.png)
![]() is the number of terms
is the number of terms ![]() times the average of the first term and the last,
times the average of the first term and the last, ![]() .
.


The picture shows that twice the sum, ![]() , so
, so ![]() .
.
General arithmetic progression
The sum of ![]() terms of an arithmetic progression
terms of an arithmetic progression ![]() is the average of the first and last terms, times the number of terms.
is the average of the first and last terms, times the number of terms.
![]()
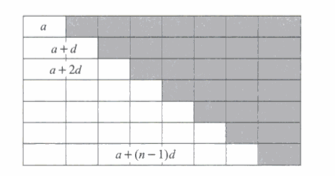
This diagram shows that ![]() is
is ![]() the size of a rectangle of height
the size of a rectangle of height ![]() and width
and width ![]() .
.
Sum of squares
![Rendered by QuickLaTeX.com \[\boxed{1^2+2^2+3^2+4^2+\dots+n^2=\frac{n(n+1)(2n+1)}{6}=\frac{n(n+\fr{2})(n+1)}{3}}\]](https://www.adamponting.com/wp-content/ql-cache/quicklatex.com-8d185be7808b4021bd6d2781e3a031db_l3.png)
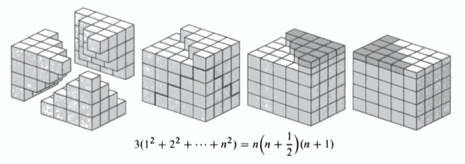
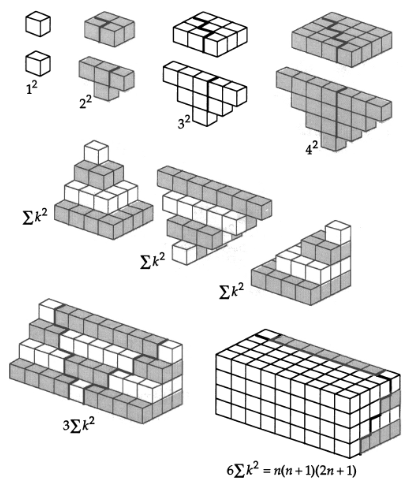
Sum of cubes

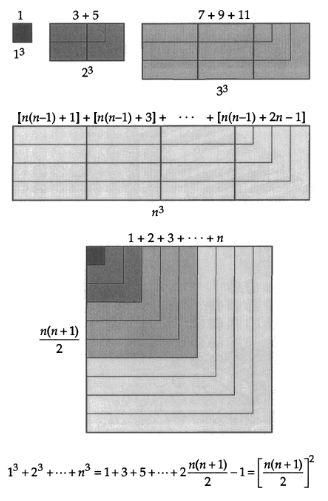
For the sum of higher powers, see Jacob Bernoulli’s power sum problem
Manipulating sums
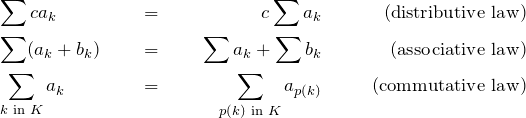
where ![]() is a permutation of the elements of
is a permutation of the elements of ![]() – i.e. the elements can be taken in any order.
– i.e. the elements can be taken in any order.
Gauss’ boyhood trick of finding ![]() can be seen as an application of these 3 laws.
can be seen as an application of these 3 laws.
To find the general sum of an arithmetic progression
![]()
We can replace ![]() by
by ![]() (commutative law):
(commutative law):
![]()
Add these 2 together. (associative law)
![]()
Take the constant outside the sum. (distributive law)
![]()
Divide this by ![]() to get:
to get:
![Rendered by QuickLaTeX.com \[S=\sum\limits_{0\les k\les n} (a+bk)=(a+\fr{2}bn)(n+1)\]](https://www.adamponting.com/wp-content/ql-cache/quicklatex.com-108df1fd0dd874d053c8a8a9eeed55d9_l3.png)
– the average of the first and last terms, ![]() , times the number of terms.
, times the number of terms.
Example of finding a sum
I wanted to make a video that starts in very slow-motion, and gradually accelerates up to 30 (different) frames a second. Maybe start with 2 images each 1/2 second long (15 frames each), then 3 images 14 frames long, 4×13, 5×12 etc until 14×3, 15 2 frames long, then return to regular 1 image per 1/30 second. How long would this take? It would take:
![]() frames/30ths of a second.
frames/30ths of a second.
If we represent the numbers rising ![]() (the number of images shown for a given number of frames, e.g. initially, 2 images last for 15 frames each) by
(the number of images shown for a given number of frames, e.g. initially, 2 images last for 15 frames each) by ![]() , then the other
, then the other ![]() is
is ![]() , and the sum is:
, and the sum is:
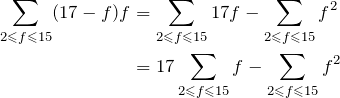
These two are the above 2 series for ![]() and
and ![]() , with only slight modification:
, with only slight modification:
![]()
![]()
So the sum can be written as:
![]() with
with ![]() , i.e.
, i.e.
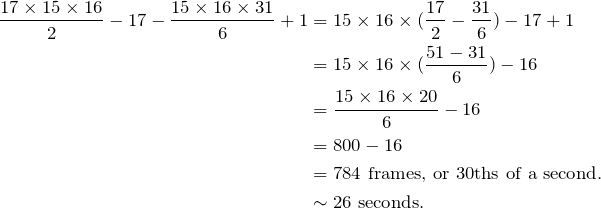
Another way using Newton’s formula:
![Rendered by QuickLaTeX.com \[\boxed{f(x)=f(0)+\Delta f(0)x+\Delta ^2f(0)\frac{\fp{x}{2}}{2!}+\Delta ^3f(0)\frac{\fp{x}{3}}{3!}+\dots}\]](https://www.adamponting.com/wp-content/ql-cache/quicklatex.com-673b5edfbc9c4badf187f7d16bb11d88_l3.png)
where ![]()
and the falling power ![]()
The sought value is a term in the series:
![]()
We need the term ending in ![]() , evidently the 14th term.
, evidently the 14th term.
Add a first term ![]() for
for ![]() , and the values in this case are:
, and the values in this case are:
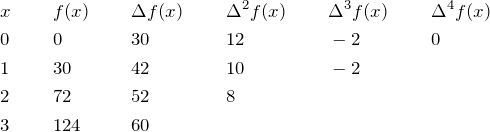
Newton’s formula gives:
![Rendered by QuickLaTeX.com \begin{align*} f(x)&=0+30\fp{x}{1}+\frac{12\fp{x}{2}}{2!}-\frac{2\fp{x}{3}}{3!} \\ &=30x+6x(x-1)-\fr{3}x(x-1)(x-2) \\ &=30x+6x^2-6x-\fr{3}(x^3-3x^2+2x) \\ &=\frac{90x+18x^2-18x-x^3+3x^2-2x}{3} \\ &=\frac{-x^3+21x^2+70x}{3} \\ &=\frac{x}{3}\Big(x(21-x)+70\Big) \\[8pt] f(14)&=\frac{14}{3}( 14 \times 7+70)=784 \end{align*}](https://www.adamponting.com/wp-content/ql-cache/quicklatex.com-6d8c4b431adac646a4d1d3b46bf2c298_l3.png)
Well, what’s the general formula, for starting with a number ![]() of images each shown for
of images each shown for ![]() 30ths of a second? i.e. the sum is then:
30ths of a second? i.e. the sum is then:
![]()
If one number from each of these pairs is ![]() , the other will be equal to
, the other will be equal to ![]() . (Like both numbers always added to 17 in the last example.)
. (Like both numbers always added to 17 in the last example.)
So this time we have
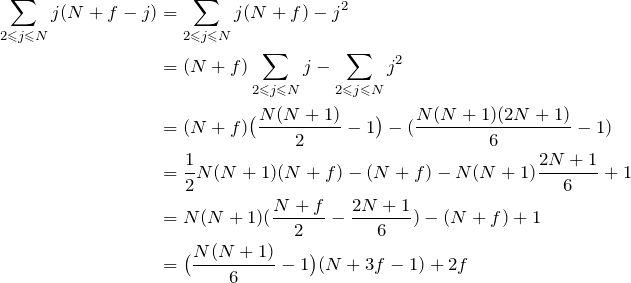
And just to check this formula, plugging in ![]() and
and ![]() :
:
![]() frames.
frames.
Knuth et al – Concrete Mathematics
